Abstract
Acute central nervous system exposure to dextroamphetamine (d-amphetamine) elicits a multitude of effects, including dual action on the dopamine transporter (DAT) to increase extracellular dopamine, and induction of a negative feedback response to limit the dopamine increase. A semimechanistic pharmacokinetic and pharmacodynamic (PK/PD) model with consideration of these multiple effects as a basis was developed. Integrated pharmacokinetics of d-amphetamine in plasma, brain extracellular fluid (ECF) via microdialysis, and cerebrospinal fluid were characterized using a population approach. This PK model was then linked to an indirect-response pharmacodynamic model using as a basis the measurement of extracellular striatal dopamine, also via microdialysis. In both rats and nonhuman primates (NHPs), d-amphetamine stimulation of dopamine outflow (reverse transport) through DAT was primarily responsible for the dose-linear increase in dopamine. As well, in both species a moderator function was needed to account for loss of the dopamine response in the presence of a relatively sustained d-amphetamine ECF exposure, presumptive of an acute tolerance response. PK/PD model structure was consistent between species; however, there was a 10-fold faster return to baseline dopamine in NHPs in response to an acute d-amphetamine challenge. These results suggest preservation from rodents to NHPs regarding the mechanism by which amphetamine increases extracellular dopamine, but a faster system response in NHPs to tolerate this increase. This microdialysis-based PK/PD model suggests greater value in directing preclinical discovery of novel approaches that modify reverse transport stimulation to treat amphetamine abuse. General value regarding insertion of an NHP model in paradigm rodent-to-human translational research is also suggested.
Introduction
Abuse of amphetamine-type stimulants (d-amphetamine, methamphetamine, and ecstasy) is a major public health threat worldwide (Krasnova and Cadet, 2009; Perez-Mana et al., 2013). The reward and reinforcing effects of these agents is a consequence of their ability to increase extracellular dopamine levels through alteration of dopamine transporter (DAT) function (Giros et al., 1996). In vitro and in vivo studies of dopaminergic neurons demonstrate that these agents manipulate DAT function by a dual mechanism: competing with extracellular dopamine for DAT-mediated reuptake into these terminals, and by stimulating reverse transport of dopamine, from nerve terminals to the extracellular fluid, through the DAT (Sulzer et al., 2005). The latter effect is mediated by a protein kinase Cβ (PKCβ)-mediated phosphorylation of DAT (Chen et al., 2009).
Given its importance in regulating dopamine-elicited behaviors, DAT function itself is subject to negative feedback regulation. This regulation has been shown to proceed via a kinase-dependent signaling cascade that couples DAT expression to the dopamine D2 autoreceptor (D2R) (Chen et al., 2013). Activation of the D2R increases DAT reuptake capacity by trafficking presynaptic terminal stores of DAT to the synaptic membranes of dopamine neurons (Bolan et al., 2007; Eriksen et al., 2010). This increased capacity to remove dopamine from synapses limits postsynaptic dopamine-elicited effects.
Amphetamine-induced stimulation of dopamine outward transport through DAT versus system response autoinhibitory feedback–enhanced reuptake through DAT are thought to occur via unique phosphorylation sites on the transporter (Zestos et al., 2016). The two effects also appear to be temporally distinct, with the amphetamine effect preceding D2R-mediated feedback (Chen et al., 2013). These asymmetric and time-dependent effects on DAT-mediated control of synaptic dopamine can presumably manifest as acute tolerance to a dose of an amphetamine-based stimulant. Acute tolerance has been demonstrated for methamphetamine in rats (Segal and Kuczenski, 2006), and for d-amphetamine in rats (Lewander, 1971), nonhuman primates (NHPs) (Jedema et al., 2014), and humans (Angrist et al., 1987; Brauer et al., 1996; Dolder et al., 2017). In vivo measurement of dopamine by microdialysis was used in rats and NHPs to evaluate these time-dependent effects. In humans, various subjective measures of mood related to the drug’s euphoric effects were observed to decline more rapidly than plasma concentrations following d-amphetamine oral doses ranging from 20 to 40 mg (Angrist et al., 1987; Brauer et al., 1996; Dolder et al., 2017). Whereas peak plasma concentrations and subjective effects occurred between 2 and 4 hours following administration, drug effect measures had largely returned to baseline values by 8 hours despite continued exposure to the drug (mean half-life = 8 hours following a 40-mg dose (Dolder et al., 2017)).
Pharmacokinetic and pharmacodynamic (PK/PD) modeling has been used to integrate drug-induced and feedback-response effects (Gabrielsson and Weiner, 2001). Advantages of this approach are that it can be used to quantify contributions of the various components of a system, and be used to simulate the impact of their alteration. To date, there has been no reported attempt to incorporate the multiple components of an acute amphetamine-mediated stimulation of dopamine release and the ensuing physiologic response to attenuate this increase. These various components are summarized in Fig. 1. Thus, the objective of the work reported was to develop a PK/PD model that systematically considered these multiple elements. To accomplish this goal, a population PK model based on d-amphetamine concentrations in plasma and two brain compartments [extracellular fluid (ECF) and cerebrospinal fluid (CSF)] was first constructed. Dextroamphetamine exposure in brain ECF was determined by quantitative microdialysis, thus providing a direct measurement of unbound, pharmacologically relevant drug concentration in this matrix. This PK model was then linked to dopamine exposure in the striatum, also measured via microdialysis, to construct the full PK/PD model. The final model provided quantitative insights in both rodent and primate species regarding the relative contributions of competitive inhibition of extracellular dopamine clearance by d-amphetamine and the drug’s stimulation of reverse transport, as well as the quantitative and temporal aspects of the system response of tolerance to this challenge in the two species.
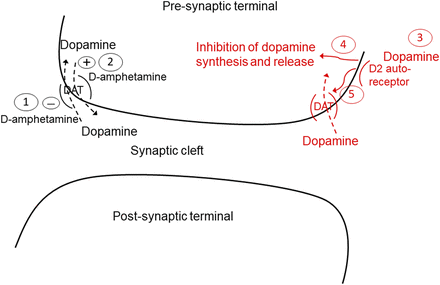
Overview of d-amphetamine action (black) and system response (red) at dopamine terminals in the striatum. Numbers refer to the following processes: (1) d-amphetamine competitive inhibition of dopamine transporter (DAT)–mediated dopamine reuptake; (2) amphetamine-evoked stimulation of reverse transport of dopamine via the DAT; (3) system response to increased synaptic dopamine is activation of the D2 autoreceptor, which can (4) inhibit dopamine synthesis and release, and/or (5) increase dopamine transporter expression in extracellular fluid–facing membranes to enhance synaptic dopamine clearance.
Materials and Methods
Materials
Dextroamphetamine sulfate was purchased from Tocris Bioscience (Avonmouth, Bristol, United Kingdom). Administered dose of 0.1 mg/kg used as a basis the free base form. Chemicals used in the preparation of intravenous formulation, microdialysis perfusion buffer, and solvents used for high-performance liquid chromatography–tandem mass spectrometry (MS/MS) analyses were of reagent grade, indicating that they conform to specifications defined by the Committee on Analytical Reagents of the American Chemical Society.
Data Sources
To support model development, a range of d-amphetamine doses was required. The live phase and sample analysis portions of studies conducted in both species following a 0.1-mg/kg i.v. bolus dose of d-amphetamine are described in detail below. Additional doses used to support PK and PD model building were obtained by digitization of mean plasma d-amphetamine and dopamine time-course data from the literature using Engauge Digitizer (https://github.com/markummitchell/engauge-digitizer/releases). For rat, this consisted of d-amphetamine exposure in plasma following 1- and 5-mg/kg i.v. bolus doses of the drug (Melega et al., 1995), and dopamine response in the striatum following intravenous bolus or subcutaneous doses ranging from 0.5 to 5 mg/kg (Kuczenski and Segal, 1989; Melega et al., 1995; Bardo et al., 1999). Male Sprague-Dawley rats were used in these studies. Mean dopamine response time courses in caudate nucleus following 0.3-, 0.5-, and 1-mg/kg i.v. bolus doses of d-amphetamine to male rhesus macaques were used to support model development in NHPs (Jedema et al., 2014). All doses for both species were used the average reported animal weights as their base, and, for PK/PD analysis, were adjusted, if necessary, to represent the free base form of d-amphetamine. Supplemental Table 1 provides an itemized summary of the various published studies from which digitized data were obtained.
Animal Preparation for Studies Conducted at 0.1-mg/kg i.v. Bolus Dextroamphetamine
All animal experiments were conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Rat experiments were conducted at the University of Groningen following approval by the Animal Care and Use Committee of that university, and were conducted in strict accordance with Dutch law, and with the European Council Directive (2010/63/EU). Experiments with NHPs were conducted at Encepharm (Germany) in strict accordance with German law, and were approved by the Lower Saxony Federal State Office for Consumer Protection and Food Safety, Germany (permit nos.: 04-076/09, 04-10/0161, and 04-11/0394).
Rat Studies.
Male Wistar rats (average weight 462 g, 12–18 weeks; Harlan, Horst, The Netherlands) were used for collection of brain ECF, CSF, and whole blood following 0.1-mg/kg d-amphetamine administration by intravenous bolus administration. Dextroamphetamine was administered through the tail vein. The formulation was sterile 0.9% sodium chloride and was administered in a volume of 0.5 ml/kg. A total of 11 animals were used in these experiments. Blood samples were collected from all animals. ECF samples for analysis of d-amphetamine were collected from four animals [microdialysis probes inserted into the medial prefrontal cortex (PFC)]. CSF samples for analysis of d-amphetamine were collected from five animals (four of which were the same as those used for ECF collection from the medial PFC). ECF samples for analysis of dopamine were collected from a separate group of five animals (microdialysis probes inserted into the caudate nucleus). After arrival, animals were housed in groups of five in polypropylene cages (40 × 50 × 20 cm) with a wire mesh top in a temperature- (22 ± 2°C) and humidity-controlled (55% ± 15%) environment on a 12-hour light cycle (07.00–19.00). After surgery, animals were housed individually (cages 30 × 30 × 30 cm). Standard diet (Diets RMH-B 2818; ABDiets, Woerden, The Netherlands) and domestic-quality water were available ad libitum.
Surgery for implantation of the microdialysis guide cannula and CSF cannula was conducted under isoflurane anesthesia (2%, with 500 ml/min O2), using bupivacaine/epinephrine for local analgesia and finadyne for peri/postoperative analgesia. To support analysis of d-amphetamine in brain ECF, a guide cannula (Brainlink B.V., Groningen, The Netherlands) was inserted into the PFC to achieve the following probe tip coordinates: anteroposterior, +3.4 mm from bregma; lateral, −0.8 mm from midline; and ventral, −5.0 mm from dura. A CSF-cannula (Brainlink) was inserted 0.45–0.55 mm deep into the cisterna magna for CSF collection. Coordinates were: anteroposterior, occipital-parietal junction; lateral, 0 mm from midline; ventral, 0.45–0.55 mm from dura. To support analysis of dopamine from brain ECF, a guide cannula was inserted into the caudate nucleus to achieve the following probe tip coordinates: anteroposterior, +0.9 mm from bregma; lateral, −3.0 mm from midline; and ventral, −6.0 mm from dura. To support analysis of d-amphetamine in plasma, a 4.2-cm indwelling cannula (Brainlink) was inserted into the jugular vein to allow for blood sampling. The cannula was exteriorized through an incision at the top of the head. Animals were allowed at least 2 days to recover from surgery. MetaQuant microdialysis probes (regenerated cellulose 18-kDa molecular weight cutoff, 216-μm outer diameter, 4-mm open dialysis membrane length (PFC), or 3-mm open dialysis membrane length (caudate nucleus) from Brainlink, were inserted 1 day before administration of d-amphetamine.
On the day of an experiment, microdialysis probes were connected with flexible PEEK tubing to a CMA 102 microdialysis pump (CMA Microdialysis, Solna, Sweden) and perfused at a rate of 0.15 μl/min with artificial CSF (147 mM NaCl, 3.0 mM KCl, 1.2 mM CaCl2, and 1.2 mM MgCl2). The slow flow design of the MetaQuant probe maximizes sample recovery, which was 106% ± 6.8% (n = 4) for d-amphetamine with results from an in vitro recovery experiment as a baseline. This result is similar to the 92% ± 5.0% from a previous study (Sood et al., 2009). That study and another (Sood et al., 2008) also compared in vivo performance of the MetaQuant probe to a standard probe design (60-kDa molecular weight cutoff, 1 μl/min). d-Amphetamine concentrations from the MetaQuant probe were similar to those in the standard probe following correction for loss in the standard probe by the no-net-flux method. Osmolarity was adjusted to approximately 300 mOsm, and pH adjusted to 7.2. The solution was autoclaved before use. Bovine serum albumin (0.2% w/v) was added to minimize solute adsorption to tubing surfaces and the probe membrane. Ultrapurified water was perfused through the dilution inlet of the probe at a flow rate of 0.8 μl/min; thus, the total dialysate flow rate was 0.95 μl/min. Following a 1-hour stabilization period, dialysate samples were collected at 30-minute intervals into polypropylene vials using an 820 Microsampler fraction collector (Univentor, Zejtun, Malta), and stored at −80°C until time of analysis. The following time points were collected, expressed as the midpoint of the collection interval, and in reference to d-amphetamine administration at 0 minutes: −75, −45, −15, 15, 45, 75, 105, 135, 165, 195, 225, 255, 285, 315 minutes.
Time points for CSF collection were −60, 0, 30, 60, 90, 120, 180, 240, and 300 minutes postadministration. Sample volume was 20 μl; these were collected into polypropylene vials and stored at −80°C until time of analysis. There was a maximum of seven samples taken from any given animal and a minimum of 1 hour between samples. Whole blood samples (150 μl) were taken at the following times from different animals, with no more than seven samples taken per animal: −60, −15, 0, 5, 10, 20, 30, 45, 60, 90, 120, 180, 240, and 300 minutes postadministration. Samples were collected into K2-EDTA tubes and placed on ice. Within 45 minutes of collection, samples were centrifuged at 4000 rpm for 10 minutes at 4°C. Resultant plasma samples were transferred to polypropylene tubes and stored at −80°C until time of analysis.
Nonhuman Primate Studies.
Male adult (4–6 years old weighing 4–6 kg) specific pathogen–free cynomolgus monkeys (Macaca fascicularis) were used (Covance GmbH, Münster, Germany). A total of three animals were used in these experiments. Dextroamphetamine was administered as a bolus dose at 0.1 mg/kg (1 ml/kg in sterile 0.9% sodium chloride) into the brachial vein via a catheter, which was subsequently flushed with approximately 1.0 ml of sterile saline. In all studies, doses were prepared fresh daily. Blood samples were taken on all dosing occasions. Brain ECF was collected simultaneously from the four probe regions (PFC and caudate nucleus from both right and left hemispheres) on one dosing occasion from one animal and used for analysis of d-amphetamine in this matrix. On three dosing occasions for the same animal, brain ECF was collected from the caudate nucleus for analysis of dopamine. CSF samples were from two separate animals on one dosing occasion.
Prior to the start of the study, all assigned animals were given a clinical examination by a veterinarian. Animals were group housed in rooms with adequate equipment for brachiating, climbing, and hiding and material for playing. The temperature was maintained above 22°C and the relative humidity at approximately 60%. Water was available ad libitum. Animals were provided with meals of balanced composition providing sufficient gross nutrients (Ssniff primate diet, Germany) and received fresh fruit and vegetables. As well, food was sometimes offered concealed so as to provide additional environmental enrichment. Following surgery, animals were single housed until completion of an experiment. In the interim between surgery and an experiment, animals were trained to sit stress-free in primate chairs so that sampling of all three matrices (plasma, brain ECF, and CSF) could be conducted in awake animals.
Coordinates for microdialysis probe placement were determined by using a magnetic resonance imaging scan, applying three-dimensional viewer software (Syngo MR B17; Siemens AG, Munich, Germany) with subsequent matching to a primate brain map (Martin and Bowden, 2000). Images were obtained with a 7-cm loop-coil in a Magnetom Trio, Tim System 3-Tesla (Siemens AG). Prior to imaging, the animal was sedated with 10 mg/kg of ketamine, 0.05 mg/kg of xylazine administered intramuscularly. Following intravenous cannulation of the brachial vein, propofol (12–15 mg/kg·h) in a volume of 10 mg/ml was started 15–30 minutes following ketamine/xylazine administration. The animal was placed in a stereotaxic frame (Kopf Model 1430; David Kopf Instruments, Tujunga, CA), with the coordinates for regions of interest defined with respect to the ear bars, which were set as anteroposterior (AP) and dorsal-ventral (DV) equal to zero. Coordinates for guide cannula placement for right and left caudate nucleus were, according to Martin and Bowden, AP: +20 mm from ear bar, mediolateral (ML): ±10.5 mm from midline, DV: 9–11 mm from dura, and for Area 46 of the right and left PFC AP: +24 mm from ear bar, ML: ±13 mm from midline, DV: 2–4 mm from the dura. Guide cannula for PFC and the caudate nucleus were 2 and 4 mm long, respectively. Tip placement for the microdialysis probe, which was the same design as used in rat studies, was 4 mm deeper than guide cannula placement. For surgical implantation of guide cannula into the four brain regions, the animal was first sedated with a ketamine/xylazine injection. Anesthesia was subsequently accomplished with isoflurane (0.8%–2% inhalation). Guide cannula placement was verified by magnetic resonance imaging within 2 weeks of surgery and immediately before a microdialysis experiment. Following surgery, 2 weeks ensued before implantation of microdialysis probes for ECF sampling. MetaQuant probes were inserted on the day of experimentation and connected to microinfusion pumps (Univentor-864; Univentor Limited) and perfused at a rate of 0.15 μl/min with artificial CSF, and water was perfused through the dilution inlet of the probe at 0.8 μl/min, as described for the rat studies. Following a 1-hour stabilization period, dialysate samples were collected at 30-minute intervals into polypropylene vials using a BASi fraction collector (West Lafayette, IN), and stored at −80°C until time of analysis. Collection was made at the following time points and expressed as the mid-point of the collection interval, in reference to d-amphetamine administration at 0 minutes: −75, −45, −15, 15, 45, 75, 105, 135, 165, 195, 225, 255, 285, 315 minutes.
CSF sampling was by a catheter that was surgically placed in the cisterna magna through the atlanto-occipital membrane, with the other end of the catheter connected to a titanium port placed between the animal’s shoulder blades. Sedation and anesthesia for catheter implantation were accomplished as described for microdialysis guide cannula implantation. The skin of an animal was incised from the posterior midline at the external occipital protuberance of the skull toward the atlas. Muscle and fat tissue were pushed outward using blunt forceps until the atlanto-occipital membrane was exposed. A small needle was pushed through the membrane and the opening enlarged using blunt forceps, until the catheter (polyurethane CNC-5POGE; Bard Peripheral Vascular, Tempe, AZ) could be placed. The catheter was fixed in place by gluing of collars on either side of the membrane. Finally, the port (Titan port CP6AC-5NC, Bard Peripheral Vascular) was connected and put into place between the shoulder blades of an animal. Animals were allowed to recover for at least 2 weeks prior to being used in an experiment. Samples (0.5 ml) were collected into polypropylene vials and stored at −80°C until time of analysis. The following time points were collected following administration of d-amphetamine: 60, 120, 180, and 240 minutes.
Sampling of whole blood (1 ml) was from a femoral or tail vein. Samples were collected into K2-EDTA tubes and placed on ice. Within 45 minutes of collection, samples were centrifuged at 4000 rpm for 10 minutes at 4°C. Resultant plasma samples were transferred to polypropylene tubes and stored at −80°C until time of analysis. The following time points were collected postadministration: 60, 120, 180, 240, 300, and 360 minutes.
Sample Analysis for Studies Conducted at 0.1-mg/kg i.v. Bolus d-Amphetamine
Dopamine and d-amphetamine concentrations were determined by high-performance liquid chromatography with tandem mass spectrometry (MS/MS) detection using appropriate internal standards (D4-dopamine and D4- phenethylamine) in separate runs. An aliquot of a solution containing each internal standard was mixed with an aliquot of each experimental sample. For analysis of dopamine, the resulting mixture was derivatized with SymDAQ automatically in the autosampler (Jacobsen et al., 2012; Hutson et al., 2015). After a predefined reaction period, an aliquot of the mixture was injected into the liquid chromatography system by an automated sample injector (SIL-20AD; Shimadzu, Japan).
Chromatographic separation was performed on a reverse-phase column (3.0 × 100 mm, particle size: 2.5 μm; Phenomenex, Torrance, CA) held at a temperature of 35–40°C. Components were separated using a linear gradient of acetonitrile containing 0.1% formic acid in ultrapurified H2O containing 0.1% formic acid (flow rate 0.3 ml/min). Mass spectrometry analyses were performed using an API 4000 MS/MS system consisting of an API 4000 MS/MS detector and a Turbo Ion Spray interface (both from Applied Biosystems, Foster City, CA). Acquisitions were performed in positive ionization mode for both d-amphetamine and dopamine, with ionization spray voltage set at 5.5 kV and a probe temperature of 400°C. The instrument was operated in multiple reaction monitoring mode. Multiple reaction monitoring transitions were 381.2 (Q1) and 338.4 (Q3) for d-amphetamine, and were 399.1 (Q1) and 175.1 (Q3) for dopamine. Suitable in-run calibration curves were fitted using weighted (1/x) regression, and the sample concentrations were determined using these calibration curves. Accuracy was verified by quality control samples after each sample series. Concentrations were calculated with the Analyst data system (Applied Biosystems). The lower limit of quantitation for d-amphetamine in 0.1 nM in brain ECF and CSF, 1 nM in plasma, and was 0.02 nM for dopamine in brain ECF.
Pharmacokinetic and Pharmacodynamic Analyses
Population pharmacokinetic analyses of d-amphetamine concentrations in the various matrices, and pharmacodynamic analyses of dopamine response in striatal ECF were conducted using Phoenix NLME (Pharsight Corporation, Certara, L.P., Princeton, NJ). Naive pool followed by nonlinear mixed effects (NLME) with first-order conditional estimation–extended least squares analyses (FOCE) were conducted. NLME-FOCE enabled estimation of intersubject and/or interoccasion variability. These population-based analyses were necessary given that samples from the three matrices for PK model development were not obtained from each animal. For PD analyses, samples for measurement of dopamine were collected from the original (0.1 mg/kg) and several published studies. The population modeling approach is able to combine such data and model it simultaneously using rigorous statistical methods (Mould and Upton, 2012).
Pharmacokinetic Model Development.
Measured (0.1 mg/kg for both species) or reported [1.0 and 5.0 mg/kg for rat (Melega et al., 1995)] plasma d-amphetamine concentrations (free + plasma protein bound) following intravenous bolus administration were converted to unbound concentrations on the basis of an unbound fraction = 0.6 in both species (Baggot et al., 1972). A one-compartment model described d-amphetamine pharmacokinetics in plasma for NHPs; whereas a two-compartment model provided the best fit for rat plasma concentrations. Following development of the plasma model, brain ECF and CSF d-amphetamine concentrations measured in both species following 0.1-mg/kg i.v. bolus administration were incorporated as peripheral compartments, with one-way ECF-to-CSF directional clearance connecting the two brain compartments. Transfer characteristics of d-amphetamine between plasma and the two brain compartments were modeled using either a single intercompartmental distributional clearance (Qbrain) or separate parameters for the uptake and efflux apparent distribution clearances (Clin and Clout). The unbound volume of distribution of d-amphetamine in the brain (Vb) was estimated using a computational approach (Spreafico and Jacobson, 2013). This approach used as a basis an estimation of Kp,uu,cell, which is the unbound intracellular concentration–to–unbound ECF concentration ratio at distributional equilibrium (Friden et al., 2011). For rats, estimation of this parameter used as a basis a Log P = 1.76 and pKa = 9.9 for d-amphetamine (www.DrugBank.ca), ECF volume = 0.2 ml/g brain (0.0072 g brain/gram body weight), brain cytoplasm volume = 0.79 ml/g brain, brain lysosome volume = 0.01 ml/g brain, pH cytoplasm = 7.0, pH lysosome = 5.0, pH ECF = 7.3, and pH blood = 7.4 (Friden et al., 2011). Rat CSF volume (Vcsf) was 0.25 ml (Cserr and Berman, 1978). For monkey, Vb and Vcsf were allometrically scaled from the rat values using the following equation: Vb,monkey = Vb,rat × (monkey weight/rat weight). A monkey weight of 5 kg and a rat weight of 0.462 kg were used, as these represented the average weights of the animals used in the 0.1-mg/kg i.v. bolus studies. Owing to correlations between Vb and BBB clearance estimates, as well as between Vcsf and Qcsf-plasma estimates (CSF volume and distributional clearance across the blood-CSF barrier, respectively), precise estimates of each could not be obtained. Thus, volume terms were frozen to achieve precise estimates of the respective clearance terms across each barrier.
Between-animal and interoccasion (plasma only) variabilities of model parameters were estimated by assuming a log-normal distribution whose basis was the exponential relationship, Pi = Ptv × exp(ηi), where Pi is the parameter estimate for the ith animal, Ptv is the population typical value, and ηi is the deviation from the population value for the ith subject. A proportional residual error model was also used to describe residual error: Cik = Predik (1 + σ), in which Cik and Predik are the measured and predicted d-amphetamine concentrations in a given matrix (ECF, CSF, or plasma) at the kth time points in the ith subject, respectively. The residual error (σ) is a random variable assumed to be normally distributed with mean zero and estimated variance σ2. Sources for this error are attributed to dosing and sampling time inaccuracies, errors in concentration analyses, and structural model misspecification.
Pharmacodynamic Model Development.
Measured or reported dopamine concentrations observed in response to d-amphetamine administration were normalized to predose (baseline) levels and expressed as percentage of baseline. At the 0.1-mg/kg dose in both species, baseline was defined as the mean of three samples taken from each animal prior to administration. The pharmacodynamic component of the full PK/PD model was added to the combined plasma-brain fluid (ECF and CSF) PK model following optimization of the combined PK model. During PD model development, PK parameter estimates were fixed. In the absence of PK data following subcutaneous administration, rapid and complete absorption of d-amphetamine from this route was assumed to include a rat study (Kuczenski and Segal, 1989) that evaluated dopamine time courses from five d-amphetamine dose levels spanning an order of magnitude, 0.5–5.0 mg/kg.
Dextroamphetamine and structurally related stimulants increase dopamine concentration in the ECF via a dual action on the DAT (Schmitt and Reith, 2010; Sulzer, 2011). As a competitive inhibitor of this transporter, amphetamine blocks the reuptake of released dopamine. Amphetamine also stimulates release from dopamine terminals via reverse transport through the DAT. Thus, the DAT is central to amphetamine-mediated increases in extracellular dopamine, and, therefore, represented the foundation of the mechanistic PD model. Representation of this dual action of d-amphetamine on extracellular dopamine is shown in Fig. 1. This two-pronged effect of amphetamine was described using an indirect response model (eq. 1), with kin representing the zero-order rate for baseline (nonstimulated) dopamine input into the extracellular space, and kout representing the rate constant for the first order (dopamine concentration-dependent) rate of dopamine removal from this space. Equation 1 describes these input and removal processes in relation to the change in extracellular dopamine concentration over time (dE/dt). 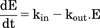 (1)The Hill equation (eq. 2) is commonly used to describe the sigmoidal relationship between drug concentration and ensuing pharmacologic effect, where Emax represents the maximum effect, C represents drug concentration, EC50 represents drug concentration responsible for 50% of the maximum effect, and γ represents the shape-factor used to adjust the steepness of the E versus C relationship.
(1)The Hill equation (eq. 2) is commonly used to describe the sigmoidal relationship between drug concentration and ensuing pharmacologic effect, where Emax represents the maximum effect, C represents drug concentration, EC50 represents drug concentration responsible for 50% of the maximum effect, and γ represents the shape-factor used to adjust the steepness of the E versus C relationship.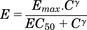 (2)This equation reduces to a linear or log-linear form when drug concentrations are sufficiently smaller than the EC50 (Gabrielsson and Weiner, 2001). Prior to development of the PD model, peak observed dopamine responses resulting from the various doses were plotted versus the corresponding time-matched predicted drug concentrations in brain extracellular fluid for both species. Results shown in Fig. 2D indicated a linear relationship. Thus, the Hill equation was reduced to eq. 3, where β represents the ratio of Emax/EC50.
(2)This equation reduces to a linear or log-linear form when drug concentrations are sufficiently smaller than the EC50 (Gabrielsson and Weiner, 2001). Prior to development of the PD model, peak observed dopamine responses resulting from the various doses were plotted versus the corresponding time-matched predicted drug concentrations in brain extracellular fluid for both species. Results shown in Fig. 2D indicated a linear relationship. Thus, the Hill equation was reduced to eq. 3, where β represents the ratio of Emax/EC50. (3)Description of the time course of dopamine in extracellular fluid used as a basis the incorporation of eq. 3 into eq. 1. Equation 4 represents the potential for d-amphetamine to act uniquely on both kin and kout components via, respectively, enhancement of reverse transport of synaptic dopamine through the DAT, and inhibition of synaptic dopamine reuptake through the DAT.
(3)Description of the time course of dopamine in extracellular fluid used as a basis the incorporation of eq. 3 into eq. 1. Equation 4 represents the potential for d-amphetamine to act uniquely on both kin and kout components via, respectively, enhancement of reverse transport of synaptic dopamine through the DAT, and inhibition of synaptic dopamine reuptake through the DAT.
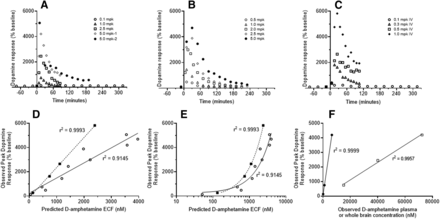
Mean striatal dopamine responses observed in rats (A and B) and NHPs (C) versus time, and in relation to predicted brain ECF D-amphetamine concentrations (D and E), and reported total plasma or whole brain concentrations (F). A, B and C: Legend refers to dose in mg/kg (mpk) reported in original work (see Supplemental Table 1 for details). In figure A, two independent studies for the 5 mpk/IV case are shown (1 from Melega et al., 1995 and 2 from Bardo et al., 1999). Data in figure B are from Kuczenski and Segal (1989). D: Mean observed peak dopamine response in relation to the time-matched predicted D-amphetamine ECF concentrations in rats (solid line, open circles) and non-human primates (dashed line, closed squares) for the various doses noted in A – C. Also shown are the correlation coefficients from linear regression analysis. E: Figure D with X-axis on the log10 scale. F: Mean observed peak dopamine response in relation to the time-matched observed D-amphetamine concentrations observed in rat plasma (closed circles from 0.1 mg/kg, and those reported by Melega et al., 1995 from 1.0 and 5.0 mg/kg) and whole brain (open squares as reported by Melega et al., 1995 from 1.0, 2.5 and 5.0 mg/kg). Correlation coefficients from linear regression analysis are also shown.
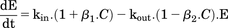 (4)
(4)Dopamine D2 autoreceptors located on presynaptic dopamine terminals regulate dopaminergic neuronal activity through multiple autoinhibitory feedback mechanisms when activated by extracellular dopamine. These include pathways that reduce dopamine availability via inhibition of its synthesis by tyrosine hydroxylase (Haubrich and Pflueger, 1982), reduction in dopamine exocytosis (L’Hirondel et al., 1998; Pothos et al., 1998), and reduced dopaminergic neuron firing (Cubeddu and Hoffmann, 1982; Jones et al., 1999). More recently, agonists of D2R have been found to increase expression of the DAT in the extracellular fluid–facing membranes of dopaminergic neurons (Bolan et al., 2007; Eriksen et al., 2010), and this occurs through accelerated DAT recycling from endosomal sites to the neuronal surface via a PKCβ-extracellular signal-regulated kinase signaling cascade (Chen et al., 2013). Such D2R-mediated increased DAT expression would enhance synaptic dopamine clearance, as DAT is the primary mechanism for dopamine removal from ECF (Chen et al., 2009). As shown in Fig. 1, autoinhibitory feedback to reduce extracellular dopamine can occur through reduced kin (decreased dopamine synthesis and release, and reduced neuronal activity) and/or enhanced kout (increased dopamine reuptake via the DAT). Including these two negative feedback mechanisms into the PK/PD model as a moderator function (M) in eq. 4 was evaluated. Equations 5a and 5b correspond to M inhibiting dopamine release into ECF, or stimulating dopamine loss from ECF, respectively.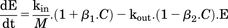 (5a)
(5a)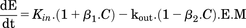 (5b)This approach is derived from the work of Bundgaard et al. (2006), who included an autoinhibitory function to describe the time course of brain ECF levels of serotonin in response to single doses of escitalopram. Applied to d-amphetamine and dopamine, increase in extracellular dopamine triggers the build-up of M, which then inhibits the synthesis and release of dopamine, or stimulates its loss from the ECF via the DAT. Build-up of M and its loss as dopamine levels return to baseline are via parallel first-order processes described by eq. 6, where ktol is the first-order rate constant governing both build-up and loss of M.
(5b)This approach is derived from the work of Bundgaard et al. (2006), who included an autoinhibitory function to describe the time course of brain ECF levels of serotonin in response to single doses of escitalopram. Applied to d-amphetamine and dopamine, increase in extracellular dopamine triggers the build-up of M, which then inhibits the synthesis and release of dopamine, or stimulates its loss from the ECF via the DAT. Build-up of M and its loss as dopamine levels return to baseline are via parallel first-order processes described by eq. 6, where ktol is the first-order rate constant governing both build-up and loss of M.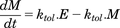 (6)In the absence of d-amphetamine, extracellular dopamine and M are constant (dE/dt = dM/dt = 0), thus E(0) = M(0) at baseline (unstimulated) conditions, and eqs. 5a and 5b reduce to eq. 7.
(6)In the absence of d-amphetamine, extracellular dopamine and M are constant (dE/dt = dM/dt = 0), thus E(0) = M(0) at baseline (unstimulated) conditions, and eqs. 5a and 5b reduce to eq. 7.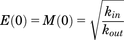 (7)The possibility that the negative feedback response depends on the duration and extent that the dopamine response is above baseline was also evaluated by implementing a series of transit compartments. This approach, which effectively buffers the feedback, is described in eqs. 8a–8c, and is similar to that used by Abraham et al. (2011) to describe the time course of parathyroid hormone in the presence of dose-related increased exposure to a negative allosteric modulator of the calcium-sensing receptor.
(7)The possibility that the negative feedback response depends on the duration and extent that the dopamine response is above baseline was also evaluated by implementing a series of transit compartments. This approach, which effectively buffers the feedback, is described in eqs. 8a–8c, and is similar to that used by Abraham et al. (2011) to describe the time course of parathyroid hormone in the presence of dose-related increased exposure to a negative allosteric modulator of the calcium-sensing receptor.
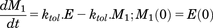 (8a)
(8a)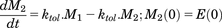 (8b)
(8b) (8c)
(8c)As with the estimated PK parameters, assessment of between-animal and interoccasion variability of pharmacodynamic parameters assumed a log-normal distribution. A proportional residual error model was also used for dopamine response observed in striatal ECF. Following identification of the best PD model structure, and apart from PK parameters that were fixed during PK model development (Vb, Clcsf, Vcsf), both PK and PD parameters were not fixed in the final combined PK/PD model analysis.
Model Evaluation.
For the PK models, linear kinetics (dose-independent clearance and volume of distribution) were observed in rat plasma over the d-amphetamine dose range evaluated, which was 0.1–5.0-mg/kg. For ECF and CSF, the various brain PK parameters were assumed to be independent of dose over this dose range to predict d-amphetamine concentrations in these two brain fluids. In NHP, linear kinetics were assumed in plasma and brain fluids over the dose range evaluated: 0.1–1.0-mg/kg. Model structure evaluation at the various model-building stages used as a basis the likelihood ratio test for nested models, with P < 0.01 used as the level of statistical significance. Akaike information criterion (AIC) was used for non-nested models, with a difference of greater than 10 considered as evidence in favor of the model with the lower AIC (Mould and Upton, 2013). For both nested and non-nested model structures, the following goodness-of-fit criteria were used: minimization of the objective function, precision of the parameter estimates, conditional weighted residuals versus time and versus population predicted amphetamine concentrations or dopamine response, and visual observation of observed amphetamine concentrations or dopamine response versus population and individual predicted amphetamine concentrations or dopamine response, respectively.
Results
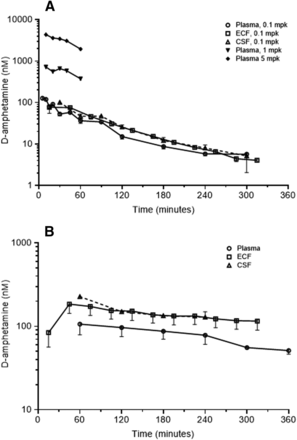
Dextroamphetamine concentrations observed in the various sampled matrices following intravenous bolus administration are summarized in Fig. 3 for both species. In both species, ECF and CSF concentrations appeared to reach distributional equilibrium with the plasma by the 1st hour, and were commonly greater than unbound plasma concentrations over most of the remaining time course. Declines in plasma concentrations in rats were similar over the 0.1- to 5-mg/kg dose range, suggesting that elimination clearance was constant over this dose range. For the three dose levels in the rat, mean terminal plasma half-life ranged from 53 minutes at 5 mg/kg (Melega et al., 1995) to 73 minutes at 0.1 mg/kg. In NHPs, mean plasma half-life was 340 minutes following the 0.1 mg/kg dose.
Mean d-amphetamine concentrations observed over time in rats (A) and NHPs (B) following a single intravenous bolus dose of d-amphetamine. (A) Concentrations in rats observed in plasma (unbound concentrations), brain ECF of the prefrontal cortex, and CSF following the indicated doses (mpk, milligrams per kilogram). For the 0.1-mg/kg dose, error bars represent S.E.M. for 1–11 rats (plasma, via a sparse sampling approach), four rats (ECF), and five rats (CSF). (B) Concentrations in NHPs observed following a 0.1-mg/kg dose in plasma (unbound concentrations, one to three animals per time point using a sparse sampling approach), brain ECF (one animal in four brain regions), and CSF (two monkeys). Error bars represent S.E.M. in plasma and ECF, and S.D. in CSF.
A two-compartment model with constant clearance over the dose range 0.1–5.0 mg/kg described systemic PK in rats. In NHPs, a one-compartment model applied. On the basis of measured d-amphetamine concentrations in brain ECF and CSF, a plasma-brain PK model was successfully constructed. In both species, transport of d-amphetamine across the BBB was best described by individual plasma-brain ECF clearance parameters, with uptake clearance (Clin) slightly larger than efflux clearance (Clout). Consistent with the much higher surface area of the BBB compared with the blood-CSF barrier, distributional clearance across the latter was fractional relative to the BBB parameters. Brain ECF-to-CSF clearance (Clcsf) could not be estimated with precision, and so was fixed 2.9 μl/min in rats and 0.6 ml/min in NHPs on the basis of preliminary naïve pool analyses. These estimates are approximately an order of magnitude larger than the reported ECF bulk flows in the two species: 0.2 μl/min in rats (de Lange, 2013) and 22 μl/min in NHPs, the latter estimate scaled from the rat value using brain weight allometry [70 g brain weight for a 5 kg animal (Sakamoto et al., 2014)]. The difference is attributed to d-amphetamine clearance into nerve terminals by DAT (Sulzer et al., 2005) and metabolism in the brain, including N-hydroxylation by brain flavin-monooxygenase (Cashman et al., 1999). Considering the same structure and comprehensive nature of the central nervous system (CNS) portion of the PK model in the two species, it has high nonclinical-to-human translational potential for prediction of human brain ECF exposure on the basis of plasma exposure and brain weight–based allometric scaling and physiologically based PK (PBPK) modeling (Yamamoto et al., 2017c).
Dopamine response time courses observed in the striatum over a range of doses are summarized in Fig. 2 for both species. As previously indicated, data from doses other than 0.1 mg/kg represent mean data obtained from published studies. Figure 2, A–C, demonstrate how dopamine response increased as d-amphetamine dose increased in both species. The time to peak response was within 30 minutes of administration in most cases in both species. In rats, the duration for the increase in dopamine over baseline was approximately 60 minutes for doses ≤1 mg/kg, and was longer than 180 minutes for two of the three 5-mg/kg doses. In the other 5-mg/kg dose study, samples were taken only out to 90 minutes (Fig. 2A). Duration of dopamine response over baseline was less than 120 minutes in NHPs following 0.1 and 0.3-mg/kg doses, and was clearly longer for the 0.5 and 1.0-mg/kg doses. In rats, the maximal increase in dopamine observed was approximately 5000% of baseline following a 5-mg/kg dose; in NHPs, the maximal response was approximately 6000% of baseline following a 1-mg/kg dose. For the two species, Fig. 2D demonstrates the linear relationship between observed peak dopamine response and the associated predicted d-amphetamine ECF concentration over the respective dose ranges; Fig. 2E presents these data on a log scale of d-amphetamine concentration, and demonstrates that responses were at the lower end of the sigmoidal exposure–response relationship. Shown in Fig. 2F is the linear relationship between observed peak dopamine concentrations and observed total plasma and whole-brain d-amphetamine concentrations over the dose range 0.1–5.0-mg/kg, thus supporting the assumption of dose-independent distribution and clearance of d-amphetamine in brain.
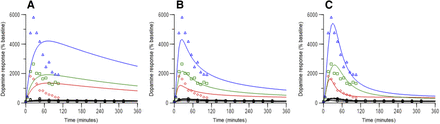
Figure 4 summarizes relationships between time-matched observed dopamine response and predicted d-amphetamine concentration in the ECF from rat studies. At doses ≥1.0 mg/kg, clockwise hysteresis was apparent, and indicates rapid equilibration between brain ECF and tissue. As well, decline in dopamine response appeared to be increasingly steeper (faster) as dose increased. As shown in Fig. 5, clockwise hysteresis was also observed at all doses in NHPs. Of note, dopamine response in NHPs declined rapidly when above 1000% of baseline, and declined relatively slower below this value. These trends in both species support a contention of acute tolerance development of the striatal dopamine system in response to a dose of d-amphetamine. On the basis of model selection criteria specified, a final model structure for both species that included a moderator function that mechanistically translated to feedback inhibition of d-amphetamine-stimulated release of dopamine was chosen. This final model structure is shown in Fig. 6. In rats, the half-life of dopamine reuptake (0.693/kout) was 2.8, and 2.2 minutes in NHP. These estimates are similar to those reported (less than 5 minutes) for negative feedback modulation of serotonin elevation in response to acute administration of escitalopram in rats (Bundgaard et al., 2006). An indirect response model with modulation on the kin side was also used for that escitalopram model.
Observed dopamine response in relation to time-matched predicted D-amphetamine ECF concentration in rats. Figures A to F represent the following respective doses as reported in the original work (see Supplemental Table 1 for details): 0.1, 0.5 (Kuczenski and Segal 1989), 1.0 (Melega et al., 1995 red circles; Kuczenski and Segal 1989 blue squares), 2.0 (Kuzcenski and Segal 1989), 2.5 (Melega et al., 1995 red circles; Kuczenski and Segal 1989 blue squares) and 5.0 mg/kg (Melega et al., 1995 red circles; Kuczenski and Segal 1989 blue squares; Bardo et al., 1999 green triangles). Individual animal data are shown in Figure A (0.1 mg/kg); mean data are shown in Figures B – F. Arrows represent the direction of increasing time after administration.
Observed dopamine response in relation to d-amphetamine ECF concentration in NHPs. Average dopamine response is in relation to time-matched predicted d-amphetamine concentrations in ECF for all doses. Circles refer to a 0.1-mg/kg dose, diamonds refer to a 0.3-mg/kg dose, triangles refer to a 0.5-mg/kg dose, and squares refer to a 1-mg/kg dose. The 0.1-mg/kg data represent the average from a single animal (n = 3 doses); whereas, for all other dose groups, mean reported data were used. The smaller figure on the right are the results from the 0.1-mg/kg dose on an expanded (y-axis) and linear (x-axis) scale; error bars represent S.E.M. All doses were by the intravenous bolus route. Arrows represent the direction of increasing time after administration.
Structure of the final PK/PD model. A two-compartment model for systemic disposition (“Peripheral d-amphetamine” compartment) applies only to the rat. Pharmacokinetic parameter definitions: Clcsf, clearance from ECF to CSF; Clin, uptake clearance from plasma to brain ECF; Clout, efflux clearance from brain ECF to plasma; Clp, clearance from the central compartment; Q, intercompartmental distribution clearance; Qcsf-plasma, distributional clearance between plasma and CSF; Vb, unbound volume of distribution in the brain; Vc, volume of central compartment; Vcsf, volume of the CSF compartment; Vp, volume of the peripheral compartment. Pharmacodynamic parameter definitions: kin, zero-order rate constant for dopamine release into the synapse; kout, first-order rate constant for dopamine reuptake into the presynaptic nerve terminal; ktol, first-order rate constant for production and dissipation of the moderator response. Buffering of the moderator response owing to dose-dependent increases in the duration and extent of the dopamine effect is indicated by the dashed outlined box, and corresponds to eq. 8a in the text. Circled numbers in the figure correspond to those used in Fig. 1.
With respect to prediction of observed dopamine response in both species, Fig. 7 summarizes observed-versus-predicted dopamine responses in the final PK/PD model. Figures 8 (rats) and 9 (NHPs) show the continuum of improved fit of dopamine time-course data by incorporating the autoinhibitory feedback function, and the final model that incorporated a single-response adjustment to this function (eq. 8a). Tables 1 and 2 summarize the estimated PK and PD parameters, respectively, in the final PK/PD model fit, and indicate that they were estimated with reasonable precision (<30%), with the exception of ktol (68.1% and 33.9% relative S.E. in rats and NHPs, respectively), and Beta associated with kin in NHPs (36.1%). The relatively lower precision of the ktol estimate is like that reported in the case of escitalopram-serotonin PK/PD modeling (Bundgaard et al., 2006), and likewise attributable to a lack of data at higher doses. In rats, interanimal/interoccasion variability was high for the central distribution volume. This is attributed to scarcity of plasma data at doses higher than 0.1 mg/kg, in particular at the early time points. Interanimal/interoccasion variability was also high for ktol in the final PD model in both rats and NHPs, and is attributed to the combination of several studies with different strains (Wistar rats at 0.1 mg/kg, and Sprague-Dawley rats the other doses) or species (cynomolgus at 0.1 mg/kg and rhesus at the other doses). Model-predicted d-amphetamine concentrations relative to those observed in the various matrices, and conditional weighted residuals for both species are summarized in Supplemental Figs. 1 and 2 for rat, and 3 and 4 for NHP.
Observed and model-predicted dopamine responses, and conditional weighted residuals for predicted dopamine responses in rats (A–D) and NHPs (E–H). Population predicted concentrations (A and E), and individual (0.1 mg/kg)/interoccasion predicted concentrations (B and F) are shown. Conditional weighted residuals are shown in relation to population-predicted values (C and G), and in relation to time (D and H).
Observed (symbols) and model predicted (lines) dopamine time courses in rats following D-amphetamine administration. Figures A – C doses to rats were 0.1 mg/kg (black circles), 1 mg/kg (red diamonds, reference 17), 2.5 mg/kg (green squares, Melega et al., 1995), 5 mg/kg (open blue triangles, solid line for study 1, Melega et al., 1995, and open blue triangles, dashed line for study 2, Bardo et al., 1999). Figures D – F doses to rats were 0.5 mg/kg (open black circles), 1 mg/kg (red diamonds), 2 mg/kg (green closed circles), 2.5 mg/kg (blue squares), 5 mg/kg (black triangles), all from Melega et al., 1995. Doses are as reported in the original work (see Supplemental Table 1 for details). Figures A and D represent no moderator component, Figures B and E represent a response-independent moderator component, and Figures C and F represent a response-adjusted moderator component in the model.
Observed (symbols) and model predicted (lines) dopamine time courses in NHPs following intravenous d-amphetamine administration. Doses to NHPs were 0.1 (black circles), 0.3 (red diamonds), 0.5 (green squares), 1.0 mg/kg (blue triangles). (A) represents no moderator component, (B) represents a response-independent moderator component, and (C) represents a response-adjusted moderator component in the model.
Population pharmacokinetic parameter estimates for dextroamphetamine in rat and nonhuman primate following dextroamphetamine administration
Parameter estimates refer to unbound d-amphetamine concentrations.
Population pharmacodynamic parameter estimates for dopamine response in rat and nonhuman primate caudate nucleus following dextroamphetamine administration
Discussion
The goal of this work was to define a PD model using as a basis a consideration of the multiple pathways by which d-amphetamine increases dopamine levels in the striatum (Hutson et al., 2014), and the negative feedback pathways employed to limit this increase (Schmitt and Reith, 2010). Most of the in vitro and in vivo research to understand d-amphetamine effects and ensuing system response have been conducted in rats; therefore, a rodent model was constructed first and guided model development in the NHP. In both species, two assumptions made in connecting the PK of d-amphetamine with dopamine response were 1) linear distribution kinetics of d-amphetamine (transfer across BBB and blood-CSF barriers, and binding/partitioning in brain), and 2) independence of BBB transfer kinetics of d-amphetamine from brain sampling site, since only the medial PFC was used for sampling of d-amphetamine in brain ECF. Results shown in Fig. 2F support the first assumption, demonstrating a linear relationship between observed dopamine response, and both observed plasma and whole brain concentrations. The second assumption was necessitated by limitation of the number of catheters/probes per animal to three. For PK studies, there was a jugular vein catheter for blood collection, one for CSF collection from the cisterna magna, and a microdialysis probe in the caudate nucleus. For dopamine studies, in addition to the jugular vein catheter, two microdialysis probes were placed in the brain, one in the medial PFC, and the other in the caudate nucleus. The physicochemical properties of d-amphetamine (Log P = 1.76, pKa = 9.9, MW = 135.2, and number of H-bond donors and acceptors both = 1) are consistent with high BBB permeability, and, combined with observed plasma-ECF distributional equilibrium within 30 minutes (Fig. 3), support rapid equilibration regardless of brain location.
Given d-amphetamine’s ability to stimulate dopamine release and prevent its reuptake, various model structures variably incorporating these two processes were evaluated. Consideration of the relative contributions of these two effects in both species occurred in the context of a linear relationship between d-amphetamine exposure and dopamine response. This linear relationship held over an approximate 50-fold increase in dopamine response over baseline in rats (5000% peak response following a 5-mg/kg dose) and 60-fold increase in NHPs (approximate peak response of 6000% following a 1-mg/kg dose). A linear relationship between d-amphetamine exposure and dopamine response, both measured in striatal ECF, was also observed in rats (Kuczenski et al., 1997). Given that pharmacologic responses eventually saturate, absence of such evidence despite the large increases observed suggests tremendous response capacity for this system in both species. Presumably, the cardiovascular effects of d-amphetamine (increased heart rate and blood pressure) prevent exploration of this limit.
Dextroamphetamine’s ability to stimulate dopamine release is reported to occur through several mechanisms (Sulzer, 2011). The pharmacodynamic parameter β-kin in the model represents the sum of these processes. Incorporation of stimulation and inhibition effects via unique pharmacodynamic parameter βs did not provide a superior fit to the dopamine time-course data relative to β-kin alone. In fact, β-kout was less than 5% relative to β-kin in both species, indicating the primary means by which d-amphetamine increases dopamine in the striatum is by stimulation of dopamine release. This conclusion agrees with findings from in vitro studies in mouse brain striatal slices demonstrating, by amperometric measures, that maximal effects of d-amphetamine exposure were dependent on dopamine release (Schmitz et al., 2001). These predicted disparate effects of d-amphetamine to increase dopamine suggest that strategies to reduce amphetamine abuse should target inhibition of its stimulation of dopamine release. Amphetamine stimulates PKCβ, resulting in enhancement of reverse transport of dopamine through DAT (Chen et al., 2009). Recent findings in rodents (Chen et al., 2013; Zestos et al., 2016) demonstrate that inhibition of PKCβ reduces amphetamine-stimulated reverse transport. Our findings of preferential amphetamine effects on reverse transport, presumably mediated through PKCβ, support this strategy. Consistency of this result in rats and NHPs furthermore enhances target validation of this potential approach to treat amphetamine abuse, including the possible use of tamoxifen, a brain permeable PKCβ inhibitor (Mikelman et al., 2017), or analogs devoid of its estrogen receptor modulation effects (Carpenter et al., 2016).
Analysis of in vitro and in vivo studies indicates that autoinhibitory feedback in dopaminergic neurons in the striatum occurs through reduced kin (decreased dopamine synthesis and release, and reduced neuronal activity) and/or enhanced kout (increased dopamine reuptake via the DAT) mechanisms. Incorporating this negative feedback by adding a moderator function to the PD model is similar to the approach used to model serotonin responses in rat hippocampus following escitalopram administration (Bundgaard et al., 2006). In both species, associating this moderator function with kin (eq. 5a) resulted in a lower AIC by greater than 10 in comparison with associating it with kout (eq. 5b), a difference that is considered statistically significant (Mould and Upton, 2013). More importantly, estimated kout in the latter case was one-third of the result obtained by associating the moderator component with kin. Mechanistically, the first order rate constant kout represents ECF dopamine clearance by diffusion of dopamine away from the microdialysis probe, and by reuptake via the DAT (Arbuthnott and Wickens, 2007). Estimates of this parameter in both species (Table 1) agree with a calculated value of 0.3 minute−1 on the basis of iontophoresis in striatum (Cragg and Rice, 2004), and agree reasonably well with estimates in rat nucleus accumbens (Raje et al., 2005). A model structure that simultaneously included moderator functions for kin and kout, achieved through unique ktol estimates for each, resulted in a lower objective function relative to the kin alone feedback model, kout had a half-life of hours, and the two ktol parameters were poorly estimated (CV >100%). Thus, acute tolerance was best described by reduction in presynaptic terminal dopamine availability and synaptic vesicle release.
The half-life associated with development and loss of tolerance was 9.6 hours in rats and 1 hour in NHPs. The rat result is similar to that obtained for tolerance to the serotonin response following escitalopram administration (Bundgaard et al., 2006). Perhaps the shorter half-life in NHPs resulted from study design at the three higher doses (Jedema et al., 2014), by which collection was halted 2 hours after administration, which is substantially shorter than the 340-minute systemic elimination half-life of d-amphetamine. Alternatively, different estimates for ktol between rats and NHPs could reflect physiologic differences between species. In this regard, studies conducted in healthy male volunteers report rapid development of tolerance to a single oral doses of Dexedrine (d-amphetamine sulfate) (Angrist et al., 1987; Brauer et al., 1996; Dolder et al., 2017). Clockwise hysteresis between PD measures and drug exposure is like the relationship observed between predicted d-amphetamine concentration in brain ECF and dopamine response in NHPs (Fig. 5). In contrast, behavioral stimulation in rodents following a single dose dissipated significantly more slowly relative to loss of ECF dopamine (Kuczenski et al., 1997). Additional studies at higher doses in both species, and certainly with longer collection times in NHPs, are needed to determine if a species difference is real. Notwithstanding, the present study substantiates availability of an NHP model to develop PK/PD models in primates linking systemic-to-brain ECF and CSF exposures to ensuing dopamine response. Its basis in a primate provides high translational potential for amphetamine stimulants, and perhaps the myriad other agents that alter central dopamine dynamics.
Microdialysis sampling to determine unbound drug concentrations in ECF has been instrumental in developing physiologic-based PK (PBPK) models of the CNS (de Lange et al., 2017; Yamamoto et al., 2017a). Recently, a generic multicompartmental CNS distribution model, including CSF compartments, was developed for the rat (Yamamoto et al., 2017b), and translated to predict human brain target site concentrations (Yamamoto et al., 2017c). Future work will pursue development of PBPK(PD) models for d-amphetamine and dopamine, including incorporation of this drug into the generic PBPK model for rats and humans, and combining with d-amphetamine metabolism and physicochemical properties. A PBPK model of d-amphetamine whose basis is NHP CNS microdialysis and a PBPKPD model in this species to predict dopamine response in striatum are also planned. In general, availability of the NHP microdialysis model with associated CSF sampling will support development of primate PBPK(PD) models.
To summarize, a PK/PD model describing the effects of acute administration of d-amphetamine on striatal dopamine levels was developed. Its structure, both in terms of suggesting the primary mechanism by which d-amphetamine increases dopamine, and the system response to limit this effect, are remarkably consistent between rodent and NHP. The model may be useful in a preclinical setting to support pharmacologic approaches to treat amphetamine abuse by limiting release of dopamine in the striatum. For example, the model could be expanded to include exposure of PKCβ inhibitors (Zestos et al., 2016), both systemically and centrally. Finally, inclusion of an NHP model within the rodent-to-human translational continuum, capable of measuring both PK and PD components of CNS-targeted drugs, could be generally useful in translational CNS research by providing increased confidence to decide whether to pursue novel drug targets.
Acknowledgments
R.E.S. thanks Dr. Serge Guzy (POP-PHARM) for his support with the Phoenix modeling language, particularly with the addition of the moderator function component to the model, and Dr. Thomas Cremers (University of Groningen) for scientific advice and encouragement toward model-based analyses.
Authorship Contributions
Participated in research design: Folgering, van Gaalen, Stratford.
Conducted experiments: Folgering, Schlumbohm, van Gaalen.
Contributed new reagents or analytical tools: Steinbach, Stratford.
Performed data analysis: Bhattacharya, Adhikari, Folgering, Steinbach, Stratford.
Wrote or contributed to the writing of the manuscript: Folgering, van Gaalen, Stratford.
Footnotes
- Received October 19, 2018.
- Accepted January 23, 2019.
↵
 This article has supplemental material available at jpet.aspetjournals.org.
This article has supplemental material available at jpet.aspetjournals.org.
Abbreviations
- AIC
- Aikake Information Criterion
- BBB
- blood-brain barrier
- CNS
- central nervous system
- CSF
- cerebrospinal fluid
- D2R
- dopamine D2 autoreceptor
- DAT
- dopamine transporter
- ECF
- extracellular fluid
- MS/MS
- tandem mass spectrometry
- NHP
- nonhuman primate
- PD
- pharmacodynamic
- PFC
- prefrontal cortex
- PK
- pharmacokinetic
- PKC
- protein kinase C
- Copyright © 2019 The Author(s).
This is an open access article distributed under the CC BY Attribution 4.0 International license.