Abstract
Dopamine exerts various effects including movement coordination and reward. It is useful to understand the quantitative relationship between drug pharmacokinetics and target engagement such as the change in occupancy and dopamine level in brain for the proper treatment of dopamine-related diseases. This study was aimed at developing a pharmacokinetic-pharmacodynamic (PK-PD) model based on dopamine transporter (DAT) occupancies that could describe changes in extracellular dopamine levels in brain after administration of methylphenidate (a DAT inhibitor) to rat. First, uptake of fluorescent substrates was studied in DAT-expressing human embryonic kidney 293 cells and concentration dependently inhibited by methylphenidate. By analyzing the uptake of fluorescent substrates in the presence or absence of methylphenidate, a mathematical model could estimate the association and dissociation rate constants of methylphenidate for DAT. Next, we measured the concentrations of methylphenidate in plasma and cerebrospinal fluid (CSF) and extracellular dopamine levels in the nucleus accumbens after single intraperitoneal administration of methylphenidate. The concentrations of methylphenidate in plasma increased almost dose proportionally and the CSF-to-plasma concentration ratio was similar among evaluated dose. The extracellular dopamine levels also increased with dose. These data were analyzed using the mechanism-based PK-PD model, which incorporates dopamine biosynthesis, release from a synapse, reuptake via DAT into a synapse, and elimination from a synapse. Methylphenidate concentrations in plasma and dopamine profiles predicted by the PK-PD model were close to in vivo observations. In conclusion, our mechanism-based PK-PD model can accurately describe dopamine levels in the brain after administration of methylphenidate to rats.
Introduction
Mechanism-based pharmacokinetic-pharmacodynamic (PK-PD) modeling has provided useful information toward understanding the quantitative relationship between drug concentrations and target engagements or pharmacological effects (Visser and Bueters, 2017). For the central nervous system acting drugs, biomarker responses and target receptor occupancy are used as indexes of target engagements for the therapeutic effect. In general, a mechanism-based PK-PD model has been developed based on data from animal experiments and in vitro assays because the availability of human biomarker responses in target tissue is limited. Yassen et al. (2006) described a different efficacy profile of buprenorphine and fentanyl using the PK-PD model based on the association and dissociation rate constants for DAT (kon and koff, respectively) for the opioid μ-receptor because it is well established that buprenorphine displays slow receptor association/dissociation kinetics in vitro as well as in vivo, causing a slow onset and long duration of the effect. Zuideveld et al. (2007) and Johnson et al. (2016) have also reported the prediction of human serotonin1A receptor–mediated responses and dopamine D2 receptor occupancy from preclinical PK-PD models. Establishing mechanism-based PK-PD modeling using preclinical information of biomarker responses and target receptor occupancy could offer a mechanistic basis of the drugs acting in the central nervous system, and eventually enable consideration of proof of concept and optimal dosage design.
Dopamine plays an important role as a neurotransmitter in pathophysiological processes. Meiser et al. (2013) summarized dopamine biosynthesis and metabolism processes. Briefly: 1) dopamine is synthesized by the combined action of tyrosine hydroxylase and aromatic amino acid decarboxylase in the neurites of dopaminergic neurons and then imported into synaptic vesicles; 2) on neuronal excitation, dopamine is released into the synaptic cleft for signal transduction; 3) dopamine is taken into dopaminergic neurons via the dopamine transporter (DAT); and 4) dopamine is metabolized to norepinephrine by dopamine β-hydroxylase or degraded by monoamine oxidase and catechol-O-methyltransferase in dopaminergic neurons. There are five different dopamine receptors, and dopamine exerts various effects including movement coordination, reward, cognition, and emotion by stimulating these receptors (Moraga-Amaro et al., 2016). Dopamine-related diseases such as attention deficit hyperactivity disorder (ADHD), Parkinson’s disease, and dementia with Lewy bodies show various physical and mental symptoms mainly due to dopamine dysfunction (Mereu et al., 2017), progressive loss of dopaminergic neurons (Ammal Kaidery and Thomas, 2018), and accumulation of Lewy bodies (Colom-Cadena et al., 2017), respectively. Drugs that regulate the dopamine level or its function in the brain have been used to treat these diseases. However, an imbalance in dopamine also causes many side effects; therefore, quantitatively understanding its relationship between drug pharmacokinetics and target engagements gives useful information when considering the therapeutic outcome.
ADHD is one of the most common neurobehavioral disorders in childhood (Briars and Todd, 2016). Amphetamine and methylphenidate are widely used as stimulant drugs for ADHD treatment. Methylphenidate inhibits both the DAT and norepinephrine transporter (Briars and Todd, 2016) and increases dopamine in the striatum and nucleus accumbens (NAc). According to Bymaster et al. (2002), atomoxetine, which is a norepinephrine transporter inhibitor, did not increase dopamine in the striatum and NAc, suggesting that methylphenidate predominantly increases dopamine in the striatum and NAc through DAT inhibition. In contrast, the pharmacological action of amphetamine is mediated by a complex mechanism including promotion of dopamine release from the dopaminergic synapse in addition to DAT inhibition (Briars and Todd, 2016). Since the pharmacological mechanism of methylphenidate has been well profiled compared with amphetamine, methylphenidate was chosen as a reference drug to establish a mechanism-based PK-PD model in order to accurately understand the correlation between dopamine behavior and DAT inhibition. Aoyama et al. (1997) reported on the results of PK-PD analysis to obtain a dopamine profile after administration of methylphenidate to rat. They analyzed the dopamine profile assuming competitive inhibition of DAT by extracellular methylphenidate concentration in the brain. However, this model did not consider the kon and koff values of methylphenidate in relation to DAT; therefore, it is not applicable to the efficacy profile characterized by slow binding kinetics, such as buprenorphine. In the present study, we focused on the dopamine profile. The kon and koff values of methylphenidate in relation to DAT were calculated using a mathematical model based on the mechanism of an in vitro fluorescence-based uptake study for DAT, and these values were incorporated into the PK-PD model to simulate the dopamine profile after administration of methylphenidate. Our objective was to investigate the mechanism-based approach to develop a PK-PD model that describes the change in dopamine levels by DAT inhibition after administration of methylphenidate to rats using DAT occupancy derived from the kon and koff values of methylphenidate.
Materials and Methods
Materials and Reagents.
Methylphenidate hydrochloride (racemic form) was purchased from Sigma-Aldrich Japan, Inc. (Tokyo, Japan). Cocaine was purchased from Takeda Pharmaceutical Company Limited (Osaka, Japan). Fluorescent-based neurotransmitter transporter uptake assay dye was obtained from Molecular Devices (Sunnyvale, CA). Saline was purchased from Otsuka Pharmaceuticals (Tokyo, Japan). All other reagents and solvents were commercial products of reagent grade.
Animals.
Animal care and all experimental procedures were performed with the approval of the Institutional Animal Care and Use Committee at Shionogi & Co., Ltd., in terms of the replacement/reduction/refinement principles. Male Crlj:WI rats were purchased at 5 weeks of age from Charles River Laboratories Japan, Inc. (Yokohama, Japan). After quarantine for a week, the rats were acclimated for several days in the animal compartment. The rats were used for the experiments at 6 weeks of age. During the acclimation and experimental periods, the rats were placed under the conditions of room temperature at 20–26°C, relative humidity at 30%–70%, and lighting for 12 hours [light (8:00 AM to 8:00 PM)/dark (8:00 Pm to 8:00 AM)], and allowed free access to tap water and solid laboratory food (CE-2; CLEA Japan, Inc.).
Fluorescence-Based Uptake Study.
Methylphenidate was dissolved in assay buffer (Hanks’ balanced salt solution containing 20 mM HEPES, 0.1% bovine serum albumin, pH 7.3) to prepare the methylphenidate solution at 0.0781–2.50 μM. Neurotransmitter assay loading dye reagent (DAT substrate) was dissolved in Hanks’ balanced salt solution containing 20 mM HEPES to prepare the loading buffer. Human embryonic kidney 293 cells stably transfected with human recombinant DAT were seeded at a density of 1 × 105 cells/ml (50 µl/well) in 384-well, clear-bottomed, black-walled plates (Greiner Bio-One, Frickenhausen, Germany) and allowed to proliferate overnight. On the day of the experiment, the culture medium was aspirated from the cell plate using a plate washer followed by addition of 20 µl assay buffer. After the plate was placed in the fluorometric imaging plate reader, the cells were incubated at room temperature for 5 minutes to capture the fluorescence at baseline. Next, both 10 µl of loading buffer and 10 µl of methylphenidate solution were added to the cells cultured on a 384-well plate, and the cells were incubated at room temperature for 90 minutes. During the incubation, fluorescence was measured every 3 seconds for the first 3 minutes and every 10 seconds for the residual 87 minutes (total points were 580 per concentration). To measure fluorescence, the dye was excited using light at a wavelength of 470–495 nm, and emission was collected at 515–575 nm. The same study was performed with cocaine (0.313 and 0.625 μM), which has the potential of DAT inhibition (Gatley et al., 1996), to support the validity of our mathematical model. The fluorescence strengths represented the mean of duplicated data.
Pharmacokinetic Study.
Rats were anesthetized with isoflurane, and a cannula was inserted into the jugular vein 4 days before the pharmacokinetic study. Methylphenidate dissolved in saline was intraperitoneally administered to conscious rats (n = 3–5/dose) at doses of 1, 3, and 6 mg/2 ml/kg using a 1-ml syringe with a 25-gauge needle. Blood (approximately 0.2 ml) was collected from the inserted cannula using a 1-ml syringe with a 23-gauge needle containing heparin and EDTA-2K at 0.033, 0.083, 0.25, 0.5, 1, 2, and 4 hours after administration. To other rats, methylphenidate solution was intraperitoneally administered (n = 3 per dose) at doses of 1, 3, and 6 mg/2 ml/kg to measure the brain and cerebrospinal fluid (CSF) concentrations of methylphenidate. The concentrations in brain were evaluated for brain penetration and the concentrations in CSF were evaluated for unbound concentration in brain. CSF was collected by inserting a 23-gauge needle connected to a syringe through a polyethylene tube into the cisterna magna at 30 minutes after collection of whole blood via the inferior vena cava. The brain was also collected from the same rats. The collected whole blood was centrifuged at 1600g for 10 minutes at 4°C to obtain plasma. The polyethylene tube for CSF sampling was washed with an equal amount of acetonitrile to prevent adsorption of the compound to the tube. Water was added to the brain samples at a ratio of brain/water = 1/3 (v/v), and the samples were homogenized. The obtained plasma, CSF, and brain samples were frozen and stored at −30°C until analysis. Methylphenidate in plasma and brain samples was extracted with acetonitrile and centrifugal separation (5000 rpm for 5 minutes at 8°C), and each supernatant was injected into a high-performance liquid chromatography–tandem mass spectrometry system using API4000 (SCIEX, Foster City, CA). The range of calibration standards was 0.5–5000 ng/ml for plasma and brain samples and 0.15–1500 ng/ml for CSF samples.
In Vivo Microdialysis Study of Dopamine Release in Nucleus Accumbens.
Rats were anesthetized with sodium pentobarbital (40 mg/kg, i.p.) and butorphanol (5 mg/kg, s.c.), and a dialysis probe (EicomCorp., Kyoto, Japan) with a guide cannula was stereotaxically implanted at the NAc shell of each rat (Anterior +1.8 mm, Lateral +0.8 mm, Ventral +6.2 mm, from the bregma and skull) (Paxinos and Watson, 1986). The cannula was cemented in place with dental acrylic, and the animal was kept warm and allowed to recover from anesthesia. Postoperative analgesia was performed by a single injection of buprenorphine (0.02 mg/kg, i.p.) (Ago et al., 2006; Sato et al., 2007). The active probe membranes were 2 mm long. Two or three days after surgery, the probe was perfused with Ringer’s solution (147.2 mM NaCl, 4.0 mM KCl, and 2.2 mM CaCl2; pH 6.0; Fuso Pharmaceutical Industries, Ltd., Osaka, Japan) at a constant flow rate of 2 μl/min and stabilized for 5 hours. Next, after methylphenidate solution had been intraperitoneally administered to conscious rats (n = 4 per dose) at doses of 1, 3, and 6 mg/2 ml/kg, microdialysis samples (12 μl) were collected every 6 minutes over 240 minutes and immediately injected to high-performance liquid chromatography analysis to determine the dopamine level, as previously reported (Koda et al., 2010; Ago et al., 2011). After the experiments, Evans Blue dye was microinjected through the cannula to histologically verify the position of the probe. Only data from animals with the correct probe placements were used for the analysis.
In Vitro Mathematical Model.
Figure 1 presents the scheme of the in vitro kinetic assay. The concentrations of fluorescent substrates (Csub) and fluorescence strength (Cflu) profiles were described using the following equations: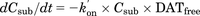 (1)
(1) (2)
(2)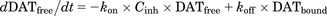 (3)
(3)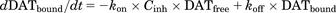 (4)where, kon′ is the permeability rate constant of the fluorescent substrates; DATfree is the unbound fraction of DAT; DATbound is the bound fraction of DAT by the DAT inhibitor; kon and koff are the association and dissociation rate constants of the DAT inhibitor, respectively; and Cinh is the concentration of DAT inhibitor (micromolars). The initial values of DATfree and DATbound are 1 and 0, respectively.
(4)where, kon′ is the permeability rate constant of the fluorescent substrates; DATfree is the unbound fraction of DAT; DATbound is the bound fraction of DAT by the DAT inhibitor; kon and koff are the association and dissociation rate constants of the DAT inhibitor, respectively; and Cinh is the concentration of DAT inhibitor (micromolars). The initial values of DATfree and DATbound are 1 and 0, respectively.
Scheme of the in vitro study. The experiment in the absence (a) or presence (b) of methylphenidate. To observe the uptake of the DAT substrate, which is composed of masking dye and fluorophore, the masking dye is removed and only the fluorophore is transported into the cell. Therefore, the transport activity of the DAT substrate was investigated by measuring the fluorescence captured from the intracellular fluorophore. To measure fluorescence, the fluorophore was excited with light at a wavelength of 470–495 nm, and emission was collected at 515–575 nm. Each parameter is defined as follows: Cinh, concentration of inhibitor; koff, dissociation rate constant of methylphenidate for DAT (per minute); k′on permeability rate constant for fluorescent substrate via DAT (per minute); kon, association rate constant of methylphenidate for DAT (micromolars per minute).
This analysis was based on two hypotheses: 1) fluorescence strength is equal to the concentration of fluorescent substrates (Csub) that penetrate through DAT and 2) at steady state, all substrates are transported via DAT (Csub at t = 0 is considered the maximum fluorescence strength).
In the absence of DAT inhibitor (Fig. 1A) DATfree was set as 1 constantly because there was no inhibitor for DAT, since fluorescent substrates mainly penetrate via all DATs into the cells and produce fluorescence. Therefore, Csub and Cflu profiles were described by the eqs. 1 and 2, and both Csub and k′on were estimated by a fitting approach based on the observed fluorescence strength profiles.
In the presence of DAT inhibitor (Fig. 1B), fluorescent substrates penetrate via only the free DAT into the cells and produce fluorescence. Therefore, the changes in Csub, Cflu, and DAT occupancy were described by the eqs. 1–4. The kon and koff values of the DAT inhibitor were estimated by a fitting approach based on the observed fluorescence strength profiles.
Mechanism-Based PK-PD Model.
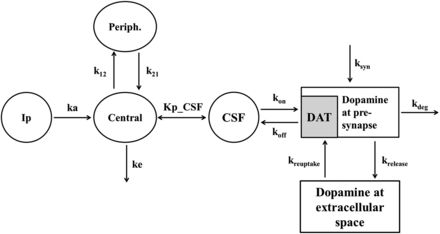
Figure 2 presents the structure of the mechanism-based PK-PD model for dopamine levels in rat brain after intraperitoneal administration of methylphenidate. Our PK-PD model was developed based on the following four points: 1) a two-compartment model for plasma concentration of methylphenidate; 2) a compartment model for CSF concentration of methylphenidate attached to the plasma compartment; 3) a component model for DAT occupancy calculated with the concentration in CSF of methylphenidate, kon, and koff; and 4) a model incorporating dopamine biosynthesis, release from a synapse, reuptake via free DAT into the synapse, and elimination from the synapse. The concentrations of methylphenidate in plasma and CSF were described by a linear two-compartment model as follows: (5)
(5) (6)
(6)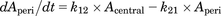 (7)
(7)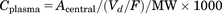 (8)
(8)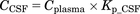 (9)where Aip, Acentral, and Aperi are the methylphenidate amounts (milligrams per kilogram) in the abdominal cavity, central, and peripheral compartments, respectively; F is the bioavailability; Vd/F is the distribution volume corrected by F of methylphenidate in the central compartment (liters per kilogram); ka, k12, k21, and ke are the first-order rate constants of absorption from the injection site, distribution to a peripheral or central compartment, and elimination from the central compartment (per minute), respectively; MW is the molecular weight of methylphenidate (233 g/mol); Cplasma is the concentration of methylphenidate in plasma (micromolars); Kp_CSF is the CSF-to-plasma concentration ratio; and CCSF is the concentration of methylphenidate in CSF.
(9)where Aip, Acentral, and Aperi are the methylphenidate amounts (milligrams per kilogram) in the abdominal cavity, central, and peripheral compartments, respectively; F is the bioavailability; Vd/F is the distribution volume corrected by F of methylphenidate in the central compartment (liters per kilogram); ka, k12, k21, and ke are the first-order rate constants of absorption from the injection site, distribution to a peripheral or central compartment, and elimination from the central compartment (per minute), respectively; MW is the molecular weight of methylphenidate (233 g/mol); Cplasma is the concentration of methylphenidate in plasma (micromolars); Kp_CSF is the CSF-to-plasma concentration ratio; and CCSF is the concentration of methylphenidate in CSF.
The structure of the PK-PD model for dopamine levels in the brain after intraperitoneal administration of methylphenidate. Each parameter is defined as follows: Central, central compartment; CSF, cerebrospinal flow compartment; DAT, DAT occupancy compartment; Ip, administration compartment; k12, first-order rate constant from the plasma to peripheral compartment; k21, first-order rate constant from the peripheral to plasma compartment; ka, absorption rate constant; kdeg, degradation rate constant of dopamine in the synapse; ke, elimination rate constant from the central compartment; krelease, first-order rate constant for dopamine release via DAT; ksyn, synthesis rate constant of dopamine in the synapse; kuptake, first-order rate constant for dopamine reuptake from the synapse; Periph, peripheral compartment.
To analyze the dopamine levels in the brain, DAT occupancy is described by eq. 10 and the dopamine levels in a synapse are described by eqs. 11 and 12: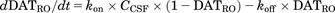 (10)
(10)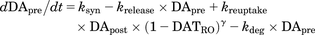 (11)
(11)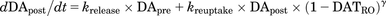 (12)where DATRO is the fraction of DAT occupied by methylphenidate in the brain; kon and koff are the in vitro association and dissociation rate constants of methylphenidate for DAT, respectively; DApre and DApost are the dopamine levels in the presynapse and extracellular space. Here, DApre_0 and DApost_0, which are the initial values of DApre and DApost, are DApost_0 × kuptake/krelease (= kuptake/krelease) and 1 (100%), respectively; ksyn is the zero-order rate constant for dopamine biosynthesis, where ksyn = kdeg × DApre_0; krelease, kuptake, and kdeg are the first-order rate constants for dopamine release from the presynapse to the extracellular space, dopamine reuptake from extracellular space to the synapse, and degradation from the synapse, respectively; and γ is the Hill coefficient.
(12)where DATRO is the fraction of DAT occupied by methylphenidate in the brain; kon and koff are the in vitro association and dissociation rate constants of methylphenidate for DAT, respectively; DApre and DApost are the dopamine levels in the presynapse and extracellular space. Here, DApre_0 and DApost_0, which are the initial values of DApre and DApost, are DApost_0 × kuptake/krelease (= kuptake/krelease) and 1 (100%), respectively; ksyn is the zero-order rate constant for dopamine biosynthesis, where ksyn = kdeg × DApre_0; krelease, kuptake, and kdeg are the first-order rate constants for dopamine release from the presynapse to the extracellular space, dopamine reuptake from extracellular space to the synapse, and degradation from the synapse, respectively; and γ is the Hill coefficient.
Data Analysis.
Pharmacokinetic analysis for the concentration of methylphenidate in plasma was performed based on a noncompartment model with uniform weighting. The area under the plasma concentration-time curve from time zero to infinity (AUC0–inf) was calculated by the trapezoidal rule. The other pharmacokinetic parameters were as follows: the maximum plasma concentration (Cmax) and time to reach the maximum plasma concentration. Pharmacodynamic analysis of dopamine level per time was also performed based on the noncompartment model with uniform weighting. The change in the area under the effect-time curve for the dopamine level from time zero to the last time was calculated by the trapezoidal rule. The maximum dopamine level and time to reach the maximum dopamine level were also calculated.
The kon and koff values of the DAT inhibitors were estimated based on the mean data of duplication. The model-dependent pharmacokinetic and PK-PD parameters were estimated by individual data for all doses to obtain the unique estimates for all parameters. For the process of PK-PD modeling, a sequential pharmacokinetic and pharmacodynamic modeling approach was applied, i.e., first the pharmacokinetic modeling was conducted, and then PK-PD modeling was performed using pharmacokinetic parameters estimated from the pharmacokinetic model to find the mean concentrations of methylphenidate in plasma.
Model-independent pharmacokinetic parameters and all model-dependent parameters were estimated using Phoenix WinNonlin (version 6.2.1; Pharsight Corp.). Model-independent pharmacodynamic parameters were calculated using Microsoft Excel 2010. Dose proportionalities were evaluated using SAS (version 9.2, SAS Institute Inc., Cary, NC) and a power model for ln-transformed Cmax and AUC0–inf.
Results
Estimation of kon and koff by In Vitro Transport Study of DAT Substrates.
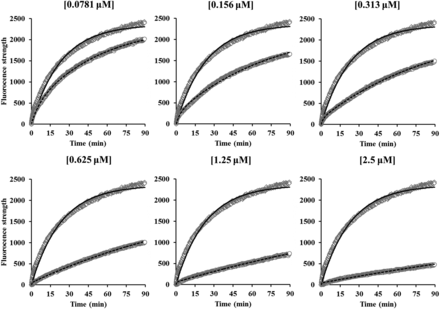
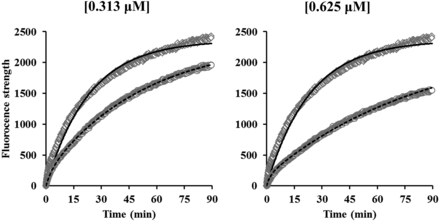
The observed fluorescent strength profiles of DAT substrates in the absence or presence of methylphenidate (0.0781–2.50 μM) are represented in Fig. 3. Fluorescent strengths of DAT substrates increased with the time and were reduced by methylphenidate in a concentration-dependent manner. These observed data showed a good fit with eqs. 1–4, and the fitting analysis resulted in the estimation of k′on, Csub, kon, and koff with CV values of less than 5% (Table 1). The dissociation constant (Kd) of methylphenidate was also calculated by koff/kon and the results are given in Table 1. Since the kon and koff values were similar at all concentrations of methylphenidate, kon (1.24 μM/min) and koff (0.129 minutes) values at 0.313 μM were selected for PK-PD modeling. The Kd value (104 nM) of methylphenidate was comparable to reported values [inhibitor constant (Ki) values of 84 ± 33 nM from Gatley et al. (1996) and 109 nM from Slusher et al. (1997)]. To confirm the validity of the model, the kon and koff values of cocaine were also evaluated. The time courses of observed fluorescent strength of DAT substrates in the absence and presence of cocaine (0.313 and 0.625 μM, respectively) are presented in Fig. 4 and the estimated parameters of cocaine are given in Table 1. The model well described the change of fluorescent strength and provided kon and koff values with CV values of less than 1.67%. The calculated Kd values for cocaine at 0.313 and 0.625 μM were 250 and 261 nM, respectively, which were close to the reported values [Ki values of 120 nM from Gatley et al. (1996) and 210 nM from Slusher et al. (1997)]. These results indicated that the kon and koff values of the DAT inhibitor could be estimated by the model, which can describe the observed fluorescent strength of DAT substrates in the absence or presence of DAT inhibitor.
The time course of observed and predicted fluorescent strength in the absence and presence of methylphenidate. The concentrations of methylphenidate were 0.0781–2.50 μM. Plots show observed data in the absence (diamonds) or presence (circles) of methylphenidate and lines show predicted data in the absence (solid lines) or presence (dashed lines) of methylphenidate.
Estimated in vitro kinetic parameters (CV%) for fluorescent substrate and methylphenidate
The time course of observed and predicted fluorescent strength in the absence and presence of cocaine. The concentrations of cocaine were 0.313 and 0.625 μM. Plots show observed data in the absence (diamonds) or presence (circles) of cocaine and lines show predicted data in the absence (solid lines) or presence (dashed lines) of cocaine.
Pharmacokinetic and Pharmacodynamic Properties of Methylphenidate in Wistar Rats.
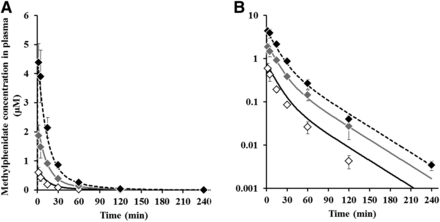
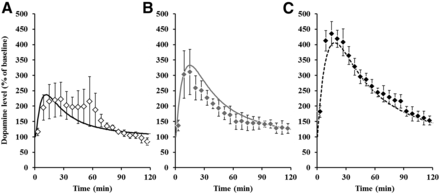
The concentration profiles of methylphenidate in plasma after intraperitoneal administration of methylphenidate at 1, 3, and 6 mg/kg are presented in Fig. 5 and the calculated pharmacokinetic parameters of methylphenidate are listed in Table 2. Methylphenidate was rapidly absorbed and showed biphasic decline with time from plasma. From the results of evaluation of dose proportionality, the slope of regression and 95% confidence intervals for Cmax were 1.13 and 0.95–1.30 and those for AUC0–inf were 1.25 and 1.15–1.36; therefore, Cmax increased almost in a dose-proportional manner but AUC0–inf increased more than dose proportionality. With intraperitoneal administration at 1, 3, and 6 mg/kg, the brain-to-plasma concentration ratio and Kp_CSF were 10.6–11.2 and 1.20–1.66, respectively, which are more than 1.0 and constant regardless of the dose. These results suggested that brain distribution of methylphenidate was high and within dose linearity up to 6 mg/kg. The dopamine profiles in NAc after intraperitoneal administration of methylphenidate at 1, 3, and 6 mg/kg are presented in Fig. 6 and each pharmacodynamic parameter is listed in Table 3. There were large interindividual variations, especially at a low dose. The times to reach the maximum dopamine levels of dopamine (16.5–25.5 minutes) were delayed compared with those of methylphenidate concentrations in plasma (2.0–2.6 minutes). Furthermore, the maximum dopamine level and change in the area under the effect-time curve for the dopamine level from time zero to the last time increased in a dose-dependent manner.
The time-course profiles of observed and predicted concentrations of methylphenidate in plasma after intraperitoneal administration in Wistar rats for pharmacokinetic study groups. Each symbol represents the observed mean ± S.D. (n = 3–5) at 1 mg/kg (open diamonds), 3 mg/kg (gray diamonds), and 6 mg/kg (black diamonds), and each line represents the predicted value at 1 mg/kg (solid lines), 3 mg/kg (gray lines), and 6 mg/kg (dashed lines). Normal scale (a) and semilog scale (b).
Pharmacokinetic parameters of methylphenidate in plasma after single intraperitoneal administration of methylphenidate to rats
Data represent mean ± S.D. (n = 3–5).
The time-course profiles of observed and predicted dopamine levels after single intraperitoneal administration of methylphenidate to Wistar rats for pharmacodynamics study groups. Each symbol represents the observed mean ± S.D. (n = 4) and each line represents the predicted value at 1 mg/kg (a), 3 mg/kg (b), and 6 mg/kg (c).
Pharmacodynamic parameters of methylphenidate in microdialysate after single intraperitoneal administration of methylphenidate to rats
Data represent mean ± S.D. (n = 4).
PK-PD Modeling for Dopamine Response.
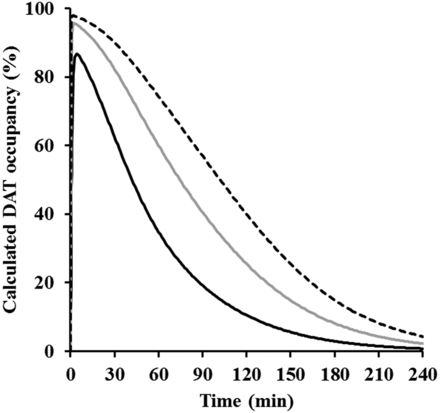
For pharmacokinetic profiles, a linear two-compartment model with first-order absorption was selected, although AUC0–inf increased more than dose proportionality because the slope of regression was not too large and the model well described the concentration of methylphenidate in plasma (Fig. 5) with reasonable variability in the estimated parameters (CV: 7.34%–38.5%, Table 4). The concentrations of methylphenidate in CSF were calculated with the concentration in plasma and Kp_CSF (eq. 9), which used the averaged value from nine rats because there was little variability among individuals and doses. The time course of calculated DAT occupancies after intraperitoneal administration of methylphenidate at 1, 3, and 6 mg/kg are presented in Fig. 7. DAT occupancies of methylphenidate showed dose dependency: the times to reach the maximum plasma concentration for the profiles of DAT occupancies were 4.0, 2.0, and 2.0 minutes (data not shown) and the plasma concentrations were 2.0–2.6 minutes, suggesting that there was little time delay between the plasma concentration profile and DAT occupancy of methylphenidate. By considering dopamine behavior in the brain and the inhibition of dopamine reuptake by methylphenidate (kon and koff), we developed the mechanism-based PK-PD model shown in Fig. 2. The model could adequately describe the change in extracellular dopamine levels in brain (Fig. 6). These results indicated that the mechanism-based PK-PD model produces optimal fit to extracellular dopamine profiles in the brain.
Parameters of methylphenidate estimated by mechanism-based pharmacokinetic and pharmacodynamic model
Calculated occupancy for dopamine transporter after intraperitoneal administration of methylphenidate at 1 mg/kg (solid line), 3 mg/kg (gray line), and 6 mg/kg (dashed line).
Discussion
For central nervous system acting drugs, a mechanism-based PK-PD model using biomarker responses and target receptor occupancy contributes to the establishment of proof of concept and pharmacological consideration by providing mechanistic information. In this aspect, a preclinical PK-PD model could be a useful tool because of limited information on biomarker responses and target receptor occupancy in humans. Since methylphenidate has been used to treat ADHD by increasing dopamine levels via inhibition of DAT in the brain, this drug was considered appropriate for developing a mechanism-based PK-PD model. In the present study, we aimed at developing a mechanism-based PK-PD model to describe dopamine levels in the brain using kon and koff of methylphenidate derived from an in vitro transport assay system.
Developing a methodology to determine the kinetics of drugs to receptors and transporters (kon and koff) offers useful information on the profiles of occupancy biomarker responses as well as pharmacodynamics (Yassen et al., 2006). For receptor kinetics, de Witte et al. (2018) have already reported the analytical methodology for the D2 receptor based on cellular response. In the present study, we focused on the transporter kinetics, and a mathematical model was developed to estimate the kon and koff values for the DAT inhibitor based on high-throughput transport assay. The Neurotransmitter Transporter Uptake Assay Kit (Molecular Devices, Sunnyvale, CA), has been used previously to calculate the IC50 values of drugs to DAT at steady state (Bernstein et al., 2012). Since this system provides a time course of fluorescent strength derived from the cellular uptake of substrates to DAT, the kinetic parameters of inhibitors to DAT were estimated by fitting for time-dependent uptake of substrates by DAT with the mathematical model. In the case of receptor-drug interaction, the kon and koff values can be estimated using the methodology of Danhof and Ploeger (2008) and de Witte et al. (2018). According to their methodology, compound and tracer or dopamine competitively bind to the target receptor and their total amounts (or concentrations) are constant in the experimental systems. On the other hand, in the case of transporter-drug interaction, the substrate is transported into the cells in one direction and the amount (or concentration) of substrate time dependently changes in the experimental buffer. Therefore, we established a new mathematical model that includes the time-dependent change of the substrate to estimate the kon and koff values for DAT based on the mechanism of DAT inhibition (eqs. 1–4). The first-order kinetic model was selected to describe the fluorescent strength while reuptake of dopamine via DAT is usually explained with the Michaelis-Menten equation (Tzvetkov et al., 2013; Dave et al., 2017). The reason is that the apparent velocity of the Michaelis-Menten equation can be approximated as Vmax/Km × (concentration) when the concentration of DAT substrate is assumed to be much lower than the Michaelis constant (Km), although the actual concentration of the DAT substrate is not disclosed because of its patent. The Kd values (104 nM for methylphenidate and 261 nM for cocaine), which are calculated using estimated kon and koff values, were comparable with published Ki values [84 ± 33 nM for methylphenidate and 120 nM for cocaine (Gatley et al., 1996) and 109 nM for methylphenidate and 210 nM for cocaine (Slusher et al., 1997)], demonstrating that the assumption is reasonable. The maximum strength of fluorescence slightly depends on sample preparation and study conditions at each examination. Therefore, Csub, which explains the maximum strength of fluorescence at steady state, was treated as a variable parameter in our model. This approach can correct the intertest variability for additional study. Human recombinant DAT was used because rat and human dopamine transporters are 92% homologous, the rank orders of Ki values of various dopamine uptake inhibitors at the human and rat dopamine transporters were highly correlated, and the Ki values of the methylphenidate in both species also were comparable (Giros et al., 1992).
Since the concentrations of methylphenidate in plasma were almost dose-proportionally increased after intraperitoneal administration of methylphenidate to rats, the concentrations were analyzed with a linear two-compartment model. The absorption rate constant was also high (ka = 7.77 minutes), presumably because the dosing route was intraperitoneal administration and methylphenidate was dissolved in saline. Even though the calculated time to reach the maximum plasma concentration using pharmacokinetic parameters (0.6 minutes) preceded the first sampling time (2 minutes), and because of the fact that the small CV percentage of ka (8.18%) and the predicted values adequately described the observed data, an absorption compartment was used for mechanistic reasons. In addition, some deviations between the predicted and observed values were obtained, especially for lower concentrations at low doses; however, the deviations were almost within 2-fold and the results were acceptable. In rats, high Kp_CSF values (1.20–1.66) and brain-to-plasma concentration ratio values (10.6–11.2) of methylphenidate were observed, suggesting that methylphenidate transfers well to the brain.
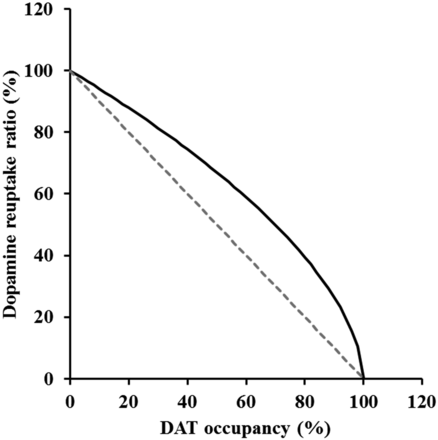
According to Aoyama et al. (1997), the estimated Ki value for methylphenidate based on extracellular fluid was consistent with the in vitro value. In addition, our concentrations of methylphenidate in CSF were comparable with their concentrations in extracellular fluid, and the drug concentration in CSF generally reflects the unbound concentration in extracellular fluid (de Lange, 2013). Therefore, DAT occupancies were calculated based on CSF concentration. In addition, Patrick et al. (1984) had reported there is little distributional delay to brain after intravenous administration of methylphenidate. Therefore, it was decided to construct the model with a CSF compartment attached to the central plasma compartment without time-delay distribution. The profiles of DAT occupancies calculated with the concentration in plasma, Kp_CSF, kon, and koff of methylphenidate, were parallel to those of plasma concentration (Fig. 7). On the other hand, the time to reach the maximum dopamine levels of the dopamine profiles was about 4- to 13-fold greater than that of DAT occupancy, and then counterclockwise hysteresis was observed between DAT occupancies and dopamine profiles (data not shown). Then, a pharmacodynamic model including the processes of dopamine biosynthesis, release from a synapse, reuptake via DAT, and metabolism had to be established to represent the behaviors of dopamine in the brain. The Vmax and Km values of the Michaelis-Menten equation for dopamine in the NAc core have been reported as 2–3 μM/s and 0.16–0.20 μM, respectively (Budygin et al., 2007), and dopamine concentrations in brain extracellular space have been reported to be 219 ± 36 pM in the hippocampus (Van Schoors et al., 2016) and 1.8 ± 0.5 nM in the medial prefrontal cortex (Faiman et al., 2013). Since the dopamine concentration in the brain extracellular space was lower than the Km value, the apparent velocity for dopamine reuptake could be approximated as Vmax/Km × (dopamine level). Therefore, the reuptake rate of dopamine was described by first-order kinetics as in the case where the kon and koff values of methylphenidate were calculated from the data of the in vitro transport assay. The estimated kuptake value was about 10-fold that of krelease, showing high activity for dopamine reuptake by DAT. The estimated krelease value was also much lower than the kon value of methylphenidate, suggesting that slow releasing of dopamine could be one of the causes for the counterclockwise hysteresis of dopamine profiles. The CV percentage of kdeg was large, possibly because there was large variability in dopamine levels, especially in the low-dose group. In addition, our analysis revealed the relationship between DAT occupancy and DAT reuptake inhibition. The Hill coefficient, which represents the degree of interaction between DAT occupancy and dopamine reuptake, was calculated as 0.578 (Table 4), indicating that nonlinear increase of extracellular dopamine levels in brain to the DAT occupancy would be suggested (Fig. 8). Consequently, the mechanism-based PK-PD model was successfully established by obtaining predicted dopamine profiles that were close to the observed ones following administration of methylphenidate to rats (Fig. 6). This is the first analytical report related to dopamine kinetics based on target occupancy; the validity of these parameters would be additional evaluation using other compounds with similar pharmacological mechanisms to methylphenidate.
The relationship between dopamine transporter occupancy and dopamine reuptake calculated using the equation: dopamine reuptake = (1 − DATRO)γ. The dashed line shows the correlation in the case of γ = 1 and the solid line shows the correlation in the case of γ = 0.578 (our result).
Dougherty et al. (1999) reported that DAT density in patients with ADHD was increased by 70% compared with healthy controls. Therefore, the pathologic condition of the disease would also need to be considered using disease model animals, such as spontaneously hypertensive rats (Heal et al., 2008). In addition, the present PK-PD model adequately predicts the dopamine profile, but its relevance for therapeutic outcome is currently unknown. Additional studies and mechanistic model development may be required to elucidate the relationship between dopamine profiles and therapeutic outcome. Furthermore, human pharmacodynamics could be predicted from animal data using an allometry approach, according to Zuideveld et al. (2007). Our model explained the behavior of dopamine using first-order rate constants, demonstrating that our model can be scaled to one describing dopamine profiles after administration of methylphenidate to humans.
In conclusion, we successfully developed a mechanism-based PK-PD model, which accurately describes the dopamine profiles in the brain after administration of methylphenidate to rats using association and dissociation rate constants derived from an in vitro transport study. These models would be useful in understanding the pharmacological effects of DAT. In future studies, the present PK-PD model needs to be further extended to predict therapeutic outcome in the consideration of proper treatment of dopamine-related diseases such as ADHD.
Acknowledgments
We thank Masaaki Sato, Satoko Funaki, Hiroko Ogawa, and Norihito Sato (Shionogi & Co., Ltd.) for technical assistance and many thoughtful suggestions.
Authorship Contributions
Participated in research design: Shimizu, Horiguchi, Yano, Shinohara, Ohnishi.
Conducted experiments: Shimizu, Horiguchi, Yano, Sakuramoto, Kanegawa.
Contributed new reagents or analytic tools: Shimizu.
Performed data analysis: Shimizu, Horiguchi.
Wrote or contributed to the writing of the manuscript: Shimizu, Horiguchi, Kanegawa, Ohnishi.
Footnotes
- Received July 29, 2018.
- Accepted January 22, 2019.
R.S., N.H., K.Y., M.S., N.K., and S.O. are full-time employees of Shionogi & Co., Ltd. S.S. is a full-time employee of Shionogi TechnoAdvanced Research Co., Ltd.
Abbreviations
- AUC0–inf
- area under the plasma concentration-time curve from time zero to infinity
- ADHD
- attention deficit hyperactivity disorder
- Cflu
- fluorescent strength
- CSF
- cerebrospinal fluid
- Csub
- concentration of fluorescent substrate
- DAT
- dopamine transporter
- Kd
- dissociation constant
- Ki
- inhibitor constant
- Km
- Michaelis constant
- koff
- dissociation rate constant for the dopamine transporter
- kon
- association rate constant for the dopamine transporter
- k′on
- permeability rate constant of fluorescent substrates
- Kp_CSF
- cerebrospinal fluid-to-plasma concentration ratio
- NAc
- nucleus accumbens
- PK-PD
- pharmacokinetic-pharmacodynamic
- Copyright © 2019 by The American Society for Pharmacology and Experimental Therapeutics