Abstract
The ataxia-telangiectasia and Rad3-related (ATR) inhibitor ceralasertib and the poly (ADP-ribose) polymerase (PARP) inhibitor olaparib have shown synergistic activity, in vitro, in the FaDu ATM-knockout cell line. It was found that combining these drugs with lower doses and for shorter treatment periods induced greater or equal toxicity in cancer cells than using either as a single agent. Here, we developed a biologically motivated mathematical model governed by a set of ordinary differential equations, considering the cell cycle–specific interactions of olaparib and ceralasertib. By exploring a range of different possible drug mechanisms, we have studied the effects of their combination as well as which drug interactions are the most prominent. After careful model selection, the model was calibrated and compared with relevant experimental data. We have used this developed model further to investigate other doses of olaparib and ceralasertib in combination, which can be potentially helpful in exploring optimized dosage and delivery.
SIGNIFICANCE STATEMENT Drugs that target cellular DNA damage repair pathways are now being used as a new way to maximize the effect of multimodality treatments such as radiotherapy. Here, we develop a mathematical model to investigate the effects of ceralasertib and olaparib, two drugs that target DNA damage response pathways.
Introduction
Recently, mathematical and computational modeling approaches have been considered as an effective and complementary way to study cancer progression and anticancer treatments as they can model cancer growth by considering cell-cell heterogeneity and dynamics (Powathil et al., 2012; Hamis et al., 2019). These in silico models can give new biological insights into cancer mechanisms and allow us to investigate the effects of anticancer treatments and study the optimal dosage, sequencing, and scheduling of them as monotherapies or in combination with one another.
Every day, each cell in the human body faces DNA damage—roughly 70,000 lesions per day (Tubbs and Nussenzweig, 2017)—which could be due to endogenous damage [such as DNA replication errors (Barnum and O’Connell, 2014)], oxidation damage (Cooke et al., 2003), and hydrolysis (De Bont and van Larebeke, 2004) or exogenous damage [such as sunlight (Barnum and O’Connell, 2014), cigarette smoking (Huang et al., 2021), and ionizing radiation (O’Connor, 2015)]. In response to DNA damage, many intracellular events are triggered to detect and repair the damage. These cellular responses are associated with the DNA damage response (DDR). The DDR is regulated by proteins responsible for detecting damage, arresting the cells to allow time for repair, activating the repair mechanisms, and inducing apoptosis if the damage is too severe for repair (Hamis et al., 2021).
The DDR consists of cell cycle checkpoints, which the cells will have to pass to enable them to continue through the cell cycle. The main checkpoints are the G1/S checkpoint, the intra-S checkpoint, and the G2/M checkpoint, which ensure that a damaged cell cannot progress through to the next phase. The activation of the cell cycle checkpoints relies heavily on the ataxia-telangiectasia mutated (ATM) and ataxia telangiectasia and Rad3-related (ATR) proteins, both of which are members of the phosphatidyilinositol-3-OH-kinases (PI3K) family (Carrassa and Damia, 2017; Hamis et al., 2021). If a damaged cell encounters a checkpoint, it should be arrested to allow time for repair (O’Connor, 2015; Ghelli Luserna di Rora’ et al., 2017). In cancer cells, certain aspects of the DDR tend to be faulty; for example, the proteins responsible for activating the checkpoints may be defective, allowing damaged DNA to pass the checkpoints and potentially cause deleterious mutations during replication and division, which could cause cancer (Barnum and O’Connell, 2014).
The most common form of DNA damage is a single-strand break (SSB), occurring approximately 55,000 times to each cell per day (O’Connor, 2015; Tubbs and Nussenzweig, 2017). The repair of SSBs heavily relies on the protein poly (ADP-ribose) polymerase (PARP)-1, which is responsible for detecting the break, binding to the break to avoid further damage, and then dissociating from the break to allow for repair (Schultz et al., 2003; Helleday, 2011; Hosoya and Miyagawa, 2014; O’Connor, 2015; Lloyd et al., 2020). Olaparib is a PARP inhibitor (PARPi) drug that inhibits the enzymatic activity of PARP1/2, meaning that PARP1 gets trapped onto the SSB, leading to inhibition of its repair (Lloyd et al., 2020).
The most cytotoxic and difficult DNA damage to repair is a double-strand break (DSB) (O’Connor, 2015), which occurs around 25 times per cell per day (Tubbs and Nussenzweig, 2017). These can arise during the replication process; for example, if an SSB is not repaired before the DNA gets duplicated, it can collide with the replication fork, causing it to stall or collapse, thus forming single-ended DSBs (seDSBs) (Helleday, 2011; Murai et al., 2012; Hosoya and Miyagawa, 2014; O’Connor, 2015; Balmus et al., 2019; Lloyd et al., 2020). These seDSBs can only be accurately repaired by the homologous recombination repair (HRR) pathway (Jelinic and Levine, 2014; Balmus et al., 2019), which works by using the identical sister chromatid as a template for repair (Delacôte and Lopez, 2008) [meaning HRR is restricted to the S and G2 phase when the sister chromatid is available (Delacôte and Lopez, 2008; Benada and Macurek, 2015)], during which single-stranded DNA overhangs are formed during the important stage of HRR, called end resection (Jasin and Rothstein, 2013; Krajewska et al., 2015). This single-stranded DNA activates ATR, emphasizing the importance of ATR in response to replication stress (Benada and Macurek, 2015; Checkley et al., 2015; Hamis et al., 2021). Nonhomologous end-joining (NHEJ), another repair pathway for DSBs that operates throughout the cell cycle, works well for double-ended DSBs by joining the two distal ends together. NHEJ works by ligating the ends of the DSB without the need for a homologous template. NHEJ is not well suited to the repair of seDSBs, because these types of breaks only have one distal end. Repair of these via NHEJ will lead to genetic rearrangements and genomic instability (Delacôte and Lopez, 2008; Davis and Chen, 2013; Chang et al., 2017).
Ceralasertib is an ATR inhibitor (ATRi) drug that inhibits the activity of ATR, causing greater reliance on the other mechanisms of the DDR [such as ATM (Lloyd et al., 2020)] (Checkley et al., 2015; Carrassa and Damia, 2017; Hamis et al., 2021). Ceralasertib plays an important role in inhibiting the repair of replication damage (Checkley et al., 2015; Hamis et al., 2021). ATR is important for activating the G2/M checkpoint, which prevents damaged cells from progressing to mitosis. When ceralasertib was given, the checkpoint became incapable of responding to damage, allowing damaged cells to bypass the checkpoint and enter mitosis. This resulted in genomic instability, leading to mitotic catastrophe (Checkley et al., 2015; Carrassa and Damia, 2017; Lloyd et al., 2020).
DDR inhibitor drugs target the cells with DDR defects, usually cancer cells, limiting the damage to noncancerous cells. The concept of synthetic lethality is that the loss/inhibition of two functions in the DDR is lethal to the cell, whereas the cell can function with the loss/inhibition of either one alone (O’Connor, 2015; O’Neil et al., 2017). For example, ATR and ATM are the primary regulators of the cell cycle checkpoints (Hamis et al., 2021). It is fairly common for diseases to have mutations in ATM (Checkley et al., 2015), which causes a greater reliance on ATR for checkpoint signaling and DNA repair (Lloyd et al., 2020). By using an ATRi drug in an ATM-deficient cancer, the cancer cells have no ATM for signaling, whereas the noncancerous cells do, thus causing damage mainly to the ATM-deficient cancer cells (Vendetti et al., 2015; Min et al., 2017; Lloyd et al., 2020). Another example of synthetic lethality is PARPi drugs in cells with breast cancer gene (BRCA) mutations. BRCA1/2 are important in HRR; hence, when a PARPi (such as olaparib) is given in a HRR-deficient cancer, the PARPi-generated seDSBs (which need HRR to be accurately repaired) will cause genomic instability because other repair pathways (such as NHEJ) will repair the damage inaccurately (Helleday, 2011; Brown et al., 2017; Lloyd et al., 2020).
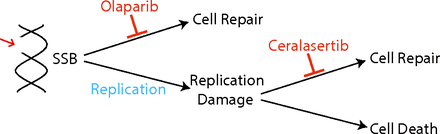
Lloyd et al. (2020) proposed synergy between ATR and PARP inhibitor drugs in ATM-deficient cancers. The synergy between PARP and ATR inhibitors is described in Fig. 1. The figure shows how olaparib inhibits the repair of SSBs, which, if not repaired before replication, can cause replication damage. In the presence of ATR, the replication damage is usually repaired. However, when ceralasertib is given, the repair is inhibited, thereby leading to cell death.
The synergy between PARP and ATR inhibitor drugs.
Here, motivated by a mechanistic cell cycle model by Checkley et al. (2015), we developed a mathematical model to further investigate the combined effects of olaparib and ceralasertib in FaDu ATM-knockout (FaDu ATM-KO) cells in vitro. The developed model incorporates appropriate biologically relevant details to explore the cell cycle–specific drug interactions and thus study the in vitro growth of the cells. The parameters are estimated using the experimental data provided by AstraZeneca (Lloyd et al., 2020).
Materials and Methods
Recently, Checkley et al. (2015) developed a mathematical model to study the effects of the ATR inhibitor drug ceralasertib alone and in combination with ionizing radiation on the cell cycle. Motivated by this model and the need for an updated model to study the effects of the ATRi drug ceralasertib and the PARPi drug olaparib as monotherapies and in combination, we developed an extended model by considering relevant biological interactions. The simulations of the model are implemented in MATLAB, and parameters have been estimated using a nonlinear least squares method, calibrating the model to experimental data provided by AstraZeneca (Lloyd et al., 2020).
Model Framework
The model represents a population of asynchronous cancer cells progressing through the cell cycle. A schematic representation is shown in Fig. 2. The green nodes represent the undamaged cells (G1, S, G2/M), the red nodes represent the damaged cells [S-damage (SD) and G2/M-damage (G2D)], and the red cross represents dead cells. Each node represents the number of cells in that state of the cell cycle.
The model: This represents cancer cells progressing through the cell cycle phases (G1, S, and G2/M nodes), where they can become damaged (SD and G2D nodes), or they can die (cross node). The arrows represent state transitions, the ki, i = 1, …, 8 values are rate constants, and the values p, q are probabilities. The value A1 represents delayed cell death, where τ represents the delay time.
No Treatment: Cell Cycle Model
Following Fig. 2, the mathematical model for the case with no drug treatment can be written as eqs. 1–6:
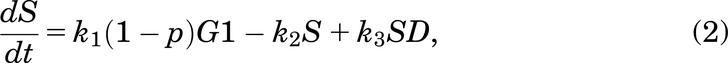
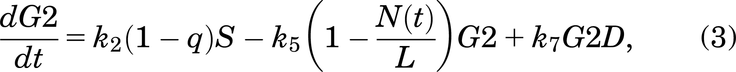
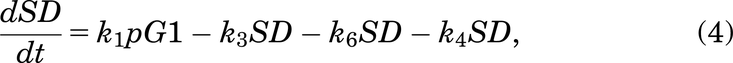
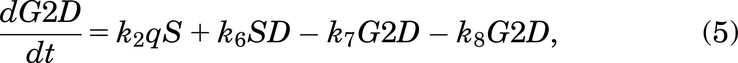
If a cell remains undamaged throughout the cell cycle, it will progress from G1 to S and then from S to G2/M, where it will divide into two daughter cells, both entering G1 (Checkley et al., 2015). A cell in the model can become damaged during replication and enter SD or during the G2/M phase and enter the G2D (Lloyd et al., 2020). From either damaged state, the cell can get repaired or die and can progress directly into G2D if in SD (O’Connor, 2015). A cell can encounter DNA damage at any point during the cell cycle, but capturing all of this, as well as various extents of damage in one mathematical model, is very elusive, so we have tried to include the main and most important aspects without making the mathematical model overly complex.
A cell will leave G1 at a rate of k1. Since all cells are at high risk of getting damaged during the replication process [e.g., from DNA replication errors (Barnum and O’Connell, 2014)], a cell will enter SD with a probability of p (and a probability of 1 − p of entering S phase with no damage). The SD compartment represents cells with replication stress (Checkley et al., 2015), mainly with seDSBs from unrepaired SSBs. A cell in SD can be repaired, represented by the transition from SD to S—this happens at a rate of k3.
We assumed that a cell in SD can enter G2D directly as cells highly depend on the G2/M checkpoint after exposure to increased damage during replication (O’Connor, 2015). ATM is important for HRR signaling and counteracting seDSB repair via NHEJ, meaning ATM deficiency has an impact on the repair of seDSBs (we attribute most of the damage in the SD compartment to be seDSBs). When ATM was deficient, HRR was delayed, and more seDSBs were repaired via NHEJ, causing aberrant chromatid fusions and cell death (Balmus et al., 2019; Lloyd et al., 2020). We assume that cells in our model are ATM-deficient, so cells in SD will likely be repaired incorrectly by NHEJ, sending them directly to G2D (at a rate of k6). If the cell is not repaired from the SD state, it may be removed from the cell cycle and enter the dead state (at a rate of k4), representing apoptosis, where it will no longer be able to progress through the cell cycle (Checkley et al., 2015).
A cell will leave the undamaged S phase at a rate of k2, but since damage can occur at any stage in the cell cycle, it is assumed that a cell can enter G2D directly from the S phase with probability q (and a probability 1 − q of entering G2/M). G2D does not represent a specific form of damage, but we assume that it will be mainly attributed to errors after replication and the unrepaired/incorrectly repaired damage from SD. Like a cell in SD, a cell in G2D can be repaired at a rate of k7. Since the G2/M checkpoint is responsible for repairing any damaged cells before they enter mitosis (Stark and Taylor, 2004; O’Connor, 2015), the repair of a cell is represented in the model by the transition from G2D to G2/M as it will need to go through the mitosis process to enable it to divide.
If the repair was not achieved for a cell in G2D, we have assumed in the model that the cell will die via mitotic catastrophe as most of the damage in this phase will represent the incorrectly repaired seDSBs, hence being removed from the system into the dead state at a rate of k8. Since we are working with in vitro data, there is only limited space for the cells to grow and divide (noting that dead cells are not removed from the system, so they still take up space). This is incorporated using a logistic growth rate,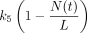 
, where k5 is the rate of a cell leaving G2/M, 
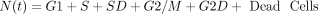is the total number of cells in the system (alive and dead), and L is the carrying capacity (Miao et al., 2016a).
Effect of the Drug Olaparib
As described in Introduction, olaparib treatment inhibits the repair of SSBs, causing indirect damage from the SSBs colliding with the replication fork, which will generate seDSBs (Murai et al., 2012; Hosoya and Miyagawa, 2014; O’Connor, 2015; Balmus et al., 2019; Lloyd et al., 2020). Hence, when olaparib treatment is added to the model, more cells will enter SD rather than S, depending on the olaparib dose [olaparib is known to be an S phase–dependent drug (Lloyd et al., 2020)]. Also, when olaparib treatment is given, FaDu ATM-KO cells accumulate in the G2 phase as arrested cells (Lloyd et al., 2020) [G2 accumulation after olaparib treatment was also found in other cell lines (Jelinic and Levine, 2014)]. In the model, we have assumed that the repair of a cell in G2D will be dose dependently inhibited by olaparib treatment.
Here, these effects (of drug) are modeled using the Sigmoid Emax equation (Greco et al., 1995) and are given by:
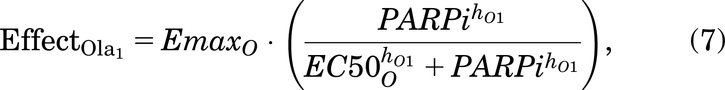
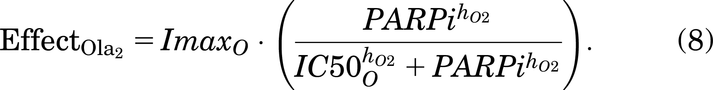
PARPi represents the concentration of the PARP inhibitor drug, olaparib.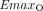 
and 
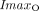represent the maximal effect and the maximal inhibitory effect of olaparib, respectively. 
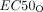and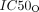 
represent the concentration of olaparib resulting in half the maximal effect and half the maximal inhibitory effect, respectively, and hO1 and hO2 represent the Hill coefficients.
The updated equations, incorporating the effects of Olaparib, are given by:
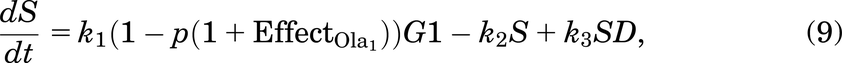
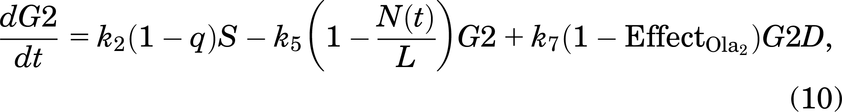
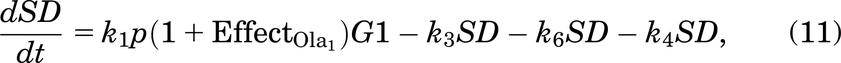
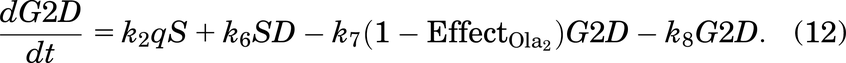
Effect of the Drug Ceralasertib
ATR is important during the repair of seDSBs via HRR and also for stabilizing and restarting stalled replication forks (Lloyd et al., 2020). Furthermore, ATR is important for activating the intra-S checkpoint, which is responsible for arresting damaged cells in the S phase and delaying the replication process (O’Connor, 2015; Lloyd et al., 2020). Hence, ceralasertib treatment dose dependently inhibits the repair of replication damage, which, in the model, is represented by the transition from SD to S at rate k3 (Checkley et al., 2015). Treatment with ceralasertib in vitro resulted in abrogation of the G2/M checkpoint [responsible for preventing damaged cells entering mitosis (Hakem, 2008)]. Thus, ceralasertib releases cells from G2 arrest, forcing them to undergo mitotic catastrophe (Checkley et al., 2015; Lloyd et al., 2020). However, drug effects are not always instantaneous (Lloyd et al., 2020); the combination of olaparib and ceralasertib could allow for shorter treatment times as they induce cell death in ATM-deficient cell lines within 1 to 2 cell divisions. Therefore, drug-induced death need not happen immediately, and this is incorporated into the model by introducing death delay. In the model, ceralasertib induces cell death from G2D as it releases cells from G2 arrest but at a delayed rate. We have introduced a transit compartment, A1, to implement death delay (Lobo and Balthasar, 2002; Miao et al., 2016a,b), which we assume is about 4 days (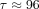
), where τ represents the time spent in the delay.
Ceralasertib drug effects are included using the Sigmoid Emax equation (Greco et al., 1995) and are given by:
ATRi represents the concentration of the ATR inhibitor drug, ceralasertib. 
and 
represent the maximal inhibitory effect and the maximal killing effect of ceralasertib, respectively. 
and 
represent the concentration of ceralasertib resulting in half the maximal inhibitory effect and half the maximal killing effect, respectively, and hC1 and hC2 represent the Hill coefficients.
The updated equations, incorporating the effects of ceralasertib are given by:
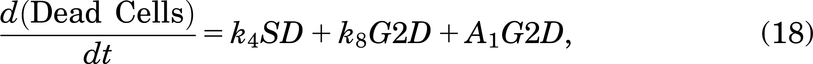
The complete model with the effects of both olaparib and ceralasertib is given in Section 1 (Model with effects of olaparib and ceralasertib) of the Supplemental Materials.
Experimental Data
The data are based on in vitro studies on FaDu ATM-KO cells (head and neck squamous cell carcinoma) (Lloyd et al., 2020). In the experiments, cells were plated at a density of 1500 cells per 384-well plate and exposed to different doses of the DDR inhibitor drugs, either alone or in combination with one another. Cells were treated with DMSO, a solvent commonly used as a vehicle in cell culture experiments, for the control case when there was no drug treatment.
Data for cell confluency and caspase 3/7 intensity confluency were collected approximately every 3 hours for 310 hours. Apoptosis was measured by mean fluorescence levels of active caspase 3/7 (calculated using incucyte ZOOM 2016A software). Using caspase 3/7 to measure cell death means that the cell death values may not be cumulative—instead, it depicts the number of dead cells at that given time point.
Implementation
Here, we assume that all cells are ATM-deficient and that they do not change in size/volume throughout the duration of the experiment. Model simulations start with an initial cell population of 1500 cells, and the full dose of the drugs is given at the start time (in line with the data). Since we are studying the case of in vitro, we may assume that the drug concentration is constant throughout the time course of our simulations (up to 310 hours) and that no drug elimination or decay happens during this time (Hamis et al., 2021).
Initial Conditions
Initial conditions were obtained from EdU pulse-chase data (Lloyd et al., 2020); namely, the percentage of cells in G1, S, and G2/M phase at t = 0 are 45.8%, 13.3%, and 39.1%, respectively. The percentage of cells in SD was estimated to be 1.57%, obtained using the experimental data of γH2AX-positive cells. The percentage of cells in G2D was approximated to be 0.23% and was calculated by finding the remainder of the cells. We start with 0 cells in the death compartment (Checkley et al., 2015).
Parameter Estimation
The parameters in the model are estimated using a nonlinear least squares method in MATLAB. Here, estimations are done using a part of the data (namely, all data except mono- and combination therapies including 0.3 μM olaparib). Estimated parameters (given in Tables 1 and 2) are then used to compare the results of other combinations that are not used in the calibration process. Appropriate sensitivity analyses were performed to study these estimated parameters [see Section 3 (Sensitivity Analysis) of the Supplemental Materials].
Table of parameters (estimated from nonlinear least squares method): The set of parameters used in Fig. 2 with their value and dimension. Here, t refers to the time in hours and N refers to the number of cells.
Table of drug-related parameters (estimated from nonlinear least squares method): The set of parameters used in Fig. 2 with their value and dimension.
To ensure a positive number of cells, we set the lower bounds of all parameters to be 0 and the upper bounds of ImaxC and ImaxO to be 1. Both probability constants were bounded at 1. By observing the cell confluency data and assuming the cells stay the same size throughout the experiment, we decided that the cell confluency, L, was less than 100,000. To avoid cells staying in the death delay for a prolonged amount of time, τ was bounded at 4 days.
Consistent with the upper bounds used in the model by Checkley et al. (2015), all rate constants ki, i = 1, 2, …, 8 were bounded at 1.0e + 06, and all hill coefficients (hO1, hO2, hC1, and hC2) were bounded at 100. To ensure a biologically relevant concentration of each drug, we bounded EC50O, IC50O, IC50C, and KC50C at 100.
When the developed model is compared against other versions of the model (to study drug effects at multiple points), the model goodness of fit was assessed using the root mean square error (RMSE):
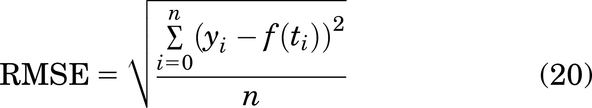where yi represents the experimental data points, and f(ti) represents the simulation value at time ti. The RMSE was calculated at each of the n experimental data points. Further, the total RMSE of each model is calculated by:
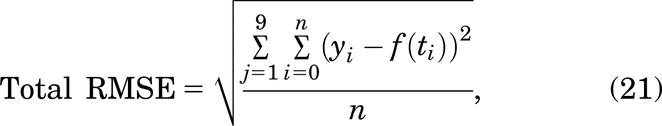where j represents each of the nine treatments.
Results
Model Analysis: Insight into Drug Interactions
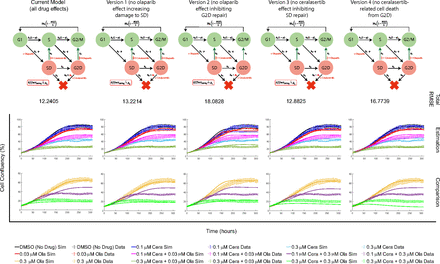
Lloyd et al. (2020) proposed synergy between ATR and PARP inhibitor drugs in ATM-deficient cancers. Both olaparib and ceralasertib exert their effects in targeting the DDR pathway at multiple points of the cell cycle (Lloyd et al., 2020). Motivated by this, the developed model incorporates the effects of these drugs at multiple points. By removing each drug effect one at a time, we can investigate which drug effects are most prominent in the model. We tested the current model described in Materials and Methods against four alternative model versions (labeled Version 1–4), each without an individual drug effect.
Figure 3 shows the current model and the four model variations that we are testing to estimate the cell confluency data. Columns 1–5 in Fig. 3 show the current model, the model without the olaparib effect in contributing to more DNA damage (model version 1), the model without olaparib inhibiting repair from G2D (model version 2), the model without ceralasertib inhibiting repair from SD (model version 3), and the model without ceralasertib-related cell death (model version 4), respectively. The first row shows a schematic of the model with total RMSE underneath, the second row shows the model calibration, and the third row shows the model validation. The estimation and comparison plots show the cell confluency over 310 hours for the simulation (solid lines) compared with the experimental data (dashed lines with error bars, mean ± S.E.M.) for each drug treatment. For each model, we optimized the parameters using the nonlinear least squares on MATLAB using a part of the data with the parameter bounds given in Parameter Estimation. The parameter values for each of these models are given in Supplemental Table 1, in Section 2 (Model Analysis: Parameter values estimated for different versions of the model) of the Supplemental Materials. For different sets of parameter values, each of these versions of the model provides a decent comparison with the experimental data. This shows that one could further simplify the developed model by omitting some of the detailed drug actions (potentially leaving the other actions more prominent). Version 2 and Version 4 of the model have the highest RMSE, illustrating the importance of both the influence of olaparib inhibiting G2D repair and the transit compartment introduced for ceralasertib-specific death delay.
Insight into drug interactions: The figure shows five variations of the model to study the role of olaparib and ceralasertib at multiple points of action. The schematic of each model is given at the top, with the cell confluency over 310 hours for all treatment types—the estimation (middle) and the comparison (bottom).
The model goodness of fit was assessed using the RMSE. Figure 4 shows the RMSE (eq. 20) of each of the nine treatments separately for each of the five models described.
The RMSE values of each of the nine treatments for each of the model variations (with and without certain drug effects). Here, the x-axis represents different treatment combinations, and the y-axis represents the RMSE value.
By comparing the individual treatment RMSE values for each of the five models (Fig. 4), it is hard to deduce which model best fits the data since different models fit different treatments better. All models are able to capture the model comparisons well, so we calculated the total RMSE (eq. 21) to see the overall RMSE for all treatment types for each model. Figure 4 also shows the total RMSE of each model, indicating that the current model gives a low RMSE among all the versions. Hence, we continue to use the current model to study the multiple effects of the drugs.
Model Calibration and Parameter Estimation
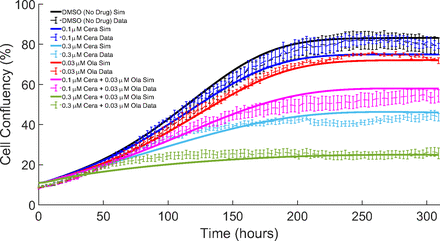
The model is first calibrated using a part of the in vitro experimental data provided by AstraZeneca (Lloyd et al., 2020) using the nonlinear least squares method on MATLAB (described in Parameter Estimation). Populations of FaDu ATM-KO cells were exposed to both the PARP inhibitor drug olaparib and the ATR inhibitor drug ceralasertib, both as monotherapies and combination therapies. Figure 5 shows the cell confluency of the in silico model (solid lines) compared with the in vitro data (dashed lines with error bars, mean ± S.E.M.) over roughly 310 hours for each treatment type (represented by different colors) involved in the optimization process. We can see from this figure that the model is capable of capturing the cell confluency data throughout the time course of the experiment. Here, we are able to capture the results from the experimental data, showing that the combination of the drugs requires lower doses and shorter treatment periods to induce growth inhibition and death of cancer cells.
Model estimation: The cell confluency over 310 hours of the simulation (solid lines) in comparison with the experimental in vitro data (dashed lines) of the treatments used for the parameter estimation. Error bars are mean ± S.E.M. (n = 3). Corresponding parameter values are given in Tables 1 and 2.
Sensitivity Analysis
We performed two uncertainty and sensitivity analyses to investigate the parameters used in the model. We performed robustness analysis and Latin hypercube analysis, which check how sensitive the model is to local and global parameter perturbations, respectively. Both methods are described in detail in Hamis et al. (2020). When investigating the model sensitivity, we take the model parameters as the input (listed in Tables 1 and 2). For the robustness analysis, we compare the cell confluency over the time course of the experiment (Supplemental Figs. 1 and 2). For the Latin hypercube analysis, the output compared is the RMSE of each treatment separately. The corresponding Pearson product moment correlation coefficients are displayed in Supplemental Fig. 3. Both the local and global analyses agree that the parameters p, L, and KC50C are the most sensitive to parameter perturbations. Details of the sensitivity analysis are described in Section 3 (Sensitivity Analysis) of the Supplemental Material.
Model Analysis: Comparing in Silico and in Vitro Results
Model Analysis: Cell Confluence Data
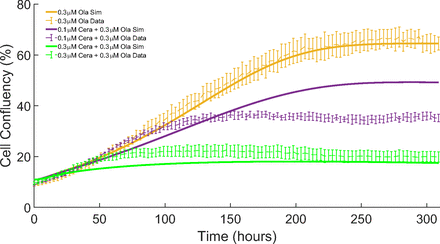
Here, we use the model together with the estimated parameters to simulate the effects of 0.3 μM olaparib and both combinations using this dose (0.1 μM ceralasertib + 0.3 μM olaparib and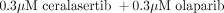 
). This is then compared with the experimental data to study the performance of the model to simulate the effects of drug combinations not previously used in the estimation process.
Figure 6 shows the in silico and in vitro comparisons of cell confluency over 310 hours for the doses not included in our parameter optimization. We can see from Fig. 6 that the model is capable of estimating the monotherapy of 0.3 μM olaparib throughout the time course of the simulation very well (orange line). It also captures very well the combination 0.3 μM ceralasertib + 0.3 μM olaparib (green line). Also, the model captures fairly well the trend of the combination of 0.1 μM ceralasertib + 0.3 μM olaparib (purple line). Overall, from both the calibration and comparison results, we see that the combination therapies result in a lower cell confluence throughout the experiments, meaning there is more growth inhibition and cell death of cancer cells.
Model Analysis: Cell Death Data
Here, we qualitatively compare the in silico results of cell death to the experimental data provided by AstraZeneca that was measured using caspase 3/7 (Lloyd et al., 2020). The experimental data shows how growth inhibition correlates with apoptosis activity. Caspase 3/7 activity was detected earlier (within 36 hours) after combination treatment, implying that apoptosis is the main reason for growth inhibition. As for single-agent treatment, caspase 3/7 activity was seen at later time points, implying that multiple rounds of cell division and/or prolonged drug exposure were needed to produce cancer growth inhibition (Lloyd et al., 2020).
The data shows the caspase 3/7–stained cells at each time point, meaning the experimental data are not cumulative like the in silico model. Therefore, both the data and simulation cell death values have been normalized between 0 and 1 for ease of comparison. Neither the details of caspase 3/7 nor cytotox markers were incorporated into the model, so we could not quantitatively compare our in silico results to the in vitro data. Instead, we showed that the mathematical model can qualitatively show the same trend as the experimental data.
Figure 7 shows the normalized cell death data measured via caspase 3/7 on the left and the normalized model simulations of cell death on the right. Each of the plots represents different drug treatments, where the black line represents no treatment, the blue line represents ceralasertib monotherapy, the red line represents olaparib monotherapy, and the green line represents combination therapy. We can see from Fig. 7 that the model is capable of capturing the cell death trend. Although the model does underestimate the amount of death after 0.1 μM ceralasertib (the data suggests a value of 0.6, whereas the simulation gives a value of roughly 0.45), overall, the model is able to qualitatively capture the trends of the cell death data measured by caspase 3/7.
Model comparison (cell death): On the left, we have the cell death measured by caspase 3/7 intensity from the experimental data, and on the right, we have the model simulation of total cell death over 310 hours. Both are normalized between 0 and 1 for ease of comparison.
Model Analysis: Investigating Drug Synergy
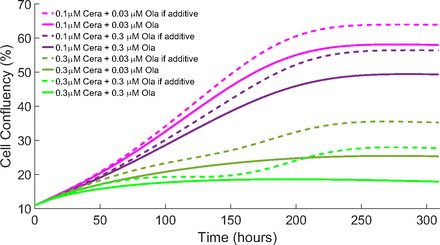
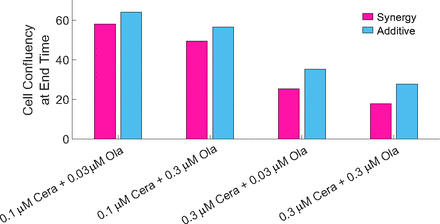
Based on the experimental evidence, Lloyd et al. (2020) proposed that there is a synergy between ATR and PARP inhibitors in ATM-deficient cancers. One way to include these effects into the model is by using an explicit synergistic drug action term (Greco et al., 1995). However, here we have not used any synergistic drug action term within the model for drug combination; hence, it is reasonable to understand whether the model does indeed show a synergistic response to the drugs studied or whether its effects are additive. To analyze this, we compared the results of the cell confluency for the model as it is now (solid lines in Fig. 8) with the results, assuming the effects were additive (dashed lines in Fig. 8). This is also evident in Fig. 9, where we visualize the cell confluency at the end time of the experiment (pink and blue bars represent the simulations synergy and the expected results if the drugs were additive).
Drug synergy: The cell confluency output of the model (solid lines) compared with if the results were additive (dashed lines) for each treatment type showing that the model is synergistic.
Drug synergy: The cell confluency output of the model at the end time of the experiment showing that the model is synergistic.
We deduced from Figs. 8 and 9 that the model shows a synergistic drug response when both drugs are combined. Here, the model results for the combinations have a lower cell confluence compared with the additive results, showing a better cell response to the drugs when combined (as seen in experimental data).
Model Analysis: Investigating Combination Therapy
Cancer is often targeted with multimodality treatments, and here, we study the effects of two DDR-inhibiting drugs that are given in combination. When such combinations are used to target cancer, it is useful to study their optimum combinations, dosage, and scheduling to maximize their effects. Here, we use the developed mathematical model, calibrated with experimental data, to investigate other combinations of olaparib and ceralasertib. Although results obtained from the modeling studies can often guide further experimental studies, any conclusions should be substantiated with experiments.
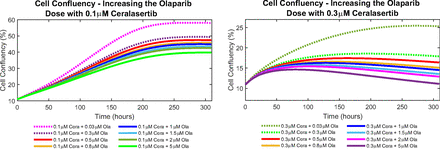
The experimental data shows that using both drugs in combination allowed for lower doses of the drugs to be used for shorter treatment periods to induce growth inhibition and cytotoxicity of cancer cells (Lloyd et al., 2020). Since we were able to capture the higher value of olaparib using the estimated parameters (see Model Analysis: Cell Confluence Data), we studied what combining even higher doses of olaparib given with both the calibrated values of ceralasertib (namely, 0.1 μM and 0.3 μM ceralasertib) would do to the cell confluency. Figure 10 shows the effect of combining 0.1 μM (left plot) and 0.3 μM (right plot) of ceralasertib with new doses of olaparib to the cell confluency over 310 hours. The dashed lines represent the combinations for which we have data. The different colored solid lines represent the newly investigated combinations, namely adding 0.5 μM, 0.8 μM, 1 μM, 1.5 μM, 2 μM, and 5 μM of olaparib to both ceralasertib doses. As expected, increasing the olaparib dose lowers the cell confluency significantly. Especially adding to 0.3 μM ceralasertib (right plot of Fig. 10), we see cell confluency values of approximately 10% (the initial confluency), showing the cytotoxic nature of the drugs. The results show that using higher doses of the drugs induced cell death and growth inhibition in a much shorter time.
Investigating combination therapy: On the left, we have the cell confluency of different doses of olaparib given with 0.1 μM ceralasertib. On the right, we have the cell confluency of different doses of olaparib given with 0.3 μM ceralasertib. Dotted lines represent the combination treatments that we have data for.
Discussion
In this study, we developed a mechanistic model representing cancer cells progressing through the cell cycle in damaged and undamaged states to account for the effects of DNA damage response pathway–inhibiting drugs. We compared the in silico results to experimental in vitro data provided by AstraZeneca (Lloyd et al., 2020). The model was adapted from a previous ordinary differential equation model developed by Checkley et al. (2015), who studied the ATR inhibitor drug ceralasertib as a monotherapy and in combination with ionizing radiation. The model was extended to study the effects and responses of olaparib and ceralasertib as monotherapies and in combination. By incorporating what we believed to be the most prominent drug interactions and damaged states into the cell cycle model, we could calibrate and validate our model.
Our in silico model results were consistent with the experimental in vitro data, showing that the combination of olaparib and ceralasertib induced greater or equal cytotoxicity and growth inhibition of cancer cells at lower doses and for shorter treatment times compared with either monotherapy. Although one could better fit the data by calibrating the model to all treatment data at once, we decided to use part of the data to compare the parameterized model results to study the model’s usefulness to simulate new combinations. The developed model showed synergistic interactions between the drugs, allowing us to study other potential doses of the drugs to optimize treatment.
We performed local and global sensitivity analysis, allowing us to study the biological mechanisms of the drugs by seeing which parameters, when perturbed by ± 20% of the optimized parameter value, affected the model output and which parameters, when varied in value, have no significant effect on the output of the model. Each drug acted in two places in the model; namely, ceralasertib both inhibited the repair of replication damage and released damaged cells from G2 arrest (releasing cells from G2D in the model). Olaparib both increased the number of damaged cells during replication and inhibited the repair of G2/M-damaged cells. The sensitivity analysis allowed us to explore how each of these drug effects affected the model by studying the parameters involved in each of the effects. The analysis implied that certain drug actions were more prominent than others, amplifying the importance of certain drug mechanisms. For example, we saw that the ceralasertib cell death–related drug effect was more important than the ceralasertib-inhibiting effect of replication damage.
Including every drug mechanism into the model and the in-depth nature of the DNA damage was elusive, so we tried capturing only the most important interactions and damage. Since our model was already fairly complex, we attempted to reduce the model by exploring different drug effects. We calibrated alternative models using only a part of the experimental data (namely, all treatments excluding 0.3 μM olaparib) and used the rest of the data to validate the model. All alternative models resulted in a larger total RMSE of all treatments, showing that the best model fit to show the synergistic interactions of olaparib and ceralasertib was the current model, with both drugs acting in two places within the model. Consistent with the sensitivity analysis, the inhibitory effects of ceralasertib affecting repair from SD to S resulted in a similar total RMSE to the current model. However, since this effect was the only drug effect in the model proposed by Checkley et al. (2015), and the RMSE was slightly worse than the current model, we decided to keep this effect to ensure there is biologic meaning to the model.
We assumed that drugs are given at the initial time of the experiment when the initial cell count is 1500 cells. There is a potential to expand this model to investigate different sequencing and schedules of the drugs to better get the optimal treatment strategy for cytotoxic and growth-inhibitory effects of cancer cells. The results from well calibrated and validated models can often guide further experimental investigations into drug doses, effects, and combinations that can result in a maximum effect while keeping the tolerated levels. However, the results from the models should be experimentally validated before any further application.
To conclude, this deterministic model, incorporating appropriate biologic details, was able to capture the quantitative nature of the cell confluency data and the qualitative trends of the cell death data found in vitro well. By doing so, we explored a range of new combinations of olaparib and ceralasertib, which cause an even greater cancer growth inhibition and more cell death. One potential future direction is to study the effects of these drugs in combination with radiation as radiation induces more DNA damage, and these DDR-inhibiting drugs reduce the likelihood of repairing any damages, thus increasing cell death. The model could be adjusted to study in vivo experimental data, allowing us to investigate optimal scheduling, sequencing, and dosage of the drugs, which can then inform clinicians on the optimal treatment of clinical trials involving olaparib and ceralasertib. Mathematical models with a similar nature to what is described in this paper, such as Checkley et al. (2015), have been used to inform starting doses of phase I clinical trials of ceralasertib monotherapy and in combination with ionizing radiation.
Acknowledgments
For the purpose of open access, the authors have applied a CC BY public copyright license to any Author Accepted Manuscript version arising. The authors thank James Yates and Sara Hamis for the constructive discussions.
Data Availability
The data that support the findings are not publicly available due to privacy or ethical restrictions.
Authorship Contributions
Participated in research design: Pugh, Davies, Powathil.
Conducted experiments: Pugh, Powathil.
Performed data analysis: Pugh, Davies, Powathil.
Wrote or contributed to the writing of the manuscript: Pugh, Davies, Powathil.
Footnotes
- Received December 15, 2022.
- Accepted May 25, 2023.
K.P. is supported by EPSRC DTP via Swansea University [Grant EP/T517987/1].
The authors declare no conflicts of interest.
↵
This article has supplemental material available at jpet.aspetjournals.org.
Abbreviations
- ATM
- ataxia-telangiectasia mutated
- ATR
- ataxia-telangiectasia and Rad3-related
- ATRi
- ATR inhibitor
- DDR
- DNA damage response
- DSB
- double-strand break
- FaDu ATM-KO
- FaDu ATM-knockout
- G2D
- G2/M-damage
- HRR
- homologous recombination repair
- NHEJ
- non-homologous end joining
- PARP
- poly (ADP-ribose) polymerase
- PARPi
- PARP inhibitor
- RMSE
- root mean square error
- SD
- S-damage
- seDSB
- single-ended DSB
- SSB
- single-strand break
- Copyright © 2023 by The American Society for Pharmacology and Experimental Therapeutics
