Abstract
It is not straightforward to simultaneously evaluate the beneficial and harmful effects of pain management, since different drugs may possess different analgesia and adverse effect profiles. Utility functions, derived from the pharmacokinetics and pharmacodynamics of individual outcome parameters, have been constructed to address this problem. Here, we construct “pragmatic” utility functions based on measurements of benefit and harm, but without making assumptions about the underlying pharmacokinetics and pharmacodynamics. Using data from two previous studies, utility functions were designed by estimating the probability of occurrence of benefit and harm and combining these into one function. Study 1 was a clinical trial on the effect of oral pregabalin on pain relief in chronic pancreatitis patients, with endpoint analgesia and dizziness monitored for 21 days. Study 2 was an experimental study on the effect of intravenous fentanyl on antinociception and respiratory depression in healthy volunteers. From study 1, the utility function was negative the first week of treatment, indicative of the greater probability of dizziness than analgesia, but positive thereafter. From study 2, the utility function showed a nadir 30 minutes after dosing, after which the probability function slowly increased toward zero. A pragmatic utility function based on the probability of two binary outcomes, analgesia and adverse effect, was successfully constructed using data from the two previous studies. The results yielded valuable insights into the utility of treatment and may be highly educative for physicians and potentially used in development of potent analgesics without serious side effects.
Introduction
Treatment of acute and chronic pain with opioid and nonopioid medication comes with adverse effects that may cause harm and limit patient and doctor compliance (Dahan et al., 2017b). Still, while some adverse effects are considered acceptable, especially when these effects are relatively minor compared with the wanted effect (analgesia), others are potentially life threatening (e.g., respiratory depression). Additionally, adverse effects may vary over time, with some increasing and others vanishing during the treatment period. How to consider the beneficial and harmful effects of treatment is often not straightforward since they may have different concentration-effect relationships. The Leiden group recently developed so-called utility or safety functions to capture opioid toxicity (e.g., potentially lethal respiratory depression, sedation, or dizziness) and benefit into one function (Yassen et al., 2008; Boom et al., 2013; Dahan et al., 2015, 2017a; Roozekrans et al., 2018). These functions are based on the economic principle that the benefit of an action (i.e., treatment with one or more specific drugs) comes at the cost of a specific harm (i.e., adverse effects) (Sheiner and Melmon, 1978). Such functions may be used early on in drug development, to compare drug utility among different patient populations, or to determine a dose regimen in specific patients in order to ensure more benefit than harm. In summary, these functions allow objective characterization of the opioid’s behavior at both ends of the spectrum.
The utility (U) functions described by Boom et al. (2013) and Roozekrans et al. (2018) were based on population pharmacokinetic-pharmacodynamic models. This enables the quantification of the utility versus (effect-site) concentration in order to simulate and predict the utility at specific clinical settings other than those under which the pharmacokinetic (PK) and pharmacodynamic (PD) data were acquired. However, there may be studies where PK-PD modeling is not part of the data analysis. For example, in the case in which drug plasma concentrations are not measured and consequently no PK model is available. For these situations, we propose constructing so-called “pragmatic” utility functions that are based on measurements of benefit and harm but make no assumptions about the underlying pharmacokinetics and pharmacodynamics. In this study, we developed these pragmatic utility functions based on data from two previous studies (Olesen et al., 2011; Boom et al., 2013).
Materials and Methods
Study Design
The first study from which data were obtained to develop a pragmatic utility function was a study on the effect of oral pregabalin on pain relief in 34 chronic pancreatitis patients, in which analgesia and dizziness were monitored for 21 days (Olesen et al., 2011). The second study was on the effect of intravenous fentanyl on anticonception and respiratory depression in 12 healthy volunteers (Boom et al., 2013). Both studies were approved by the local institutional review boards, and written informed consent was obtained from all subjects prior to participation in the trial.
Study 1.
Sixty-four patients with moderate to severe pain from chronic pancreatitis were randomized to receive increasing oral doses of the gabapentoid pregabalin or placebo for 3 weeks. The initial pregabalin/placebo dose was 75 mg twice daily; on day 3 the dose was increased to 150 mg twice daily, and finally on day 7 the dose was increased to 300 mg twice daily. In the case of unacceptable adverse effects, the dose could be adjusted to the previous dose [i.e., from 300 to 150 mg or 150 to 75 mg (twice daily)]. For the construction of the utility functions, we used data of the 34 patients that received active medication: 21 men and 13 women (age 52 ± 10 years, duration of pancreatitis 8.5 ± 6.2 years). Maximum daily pain score was 5.8 ± 2.3 points on an 11-point numerical rating scale from 0 (no pain) to 10 (most severe pain imaginable). Pain scores and adverse effects (including dizziness, scored as a binary outcome) were obtained on days 0 (pretreatment baseline), 4, 7, 11, 14, 17, and 21 of treatment.
Study 2.
Twelve healthy male volunteers (aged 18–25 years, body mass index 20–28 kg/m2) received a bolus fentanyl infusion of 3.5 µg/kg on two separate occasions. On the first study day, the influence of fentanyl on isohypercapnic ventilation was measured for 6 hours using the “dynamic end-tidal forcing” technique (for explanation of the technique, see Dahan et al., 2007). End-tidal PCO2 was clamped such that ventilation was 20 ± 2 l/min prior to fentanyl administration. On the second study day, the effect of fentanyl on pain tolerance to an electrical stimulus was measured for 6 hours. A noxious electrical stimulus train was applied using a custom-made computer-interfaced constant current stimulator. The current was increased from 0 mA at 0.5 mA/s until the subject pressed a control button at pain tolerance, at which the stimulus train ended.
Construction of the Pragmatic Utility Function
To construct utility functions, both harm (H) and benefit (B) were treated as binary outcomes: these occurred or did not occur. The probability P that a binary outcome occurs is estimated by the proportion denoted by probability π. Thus, π is calculated as the number of subjects in which the outcome occurs divided by the number of subjects (n). The variance (var) of the proportion is given by var{π} = π ⋅ (1 − π)/n.
In study 1, benefit was significant analgesia and harm was dizziness. Significant analgesia was defined as a pain score that is lower than 50% of the baseline score (i.e., a pain score reduction >50%). The proportion of subjects having significant analgesia at time t is denoted by πB(t); the proportion of subjects experiencing dizziness is denoted by πH(t). Similarly, in study 2, B was significant antinociception (a 50% increase in electrical pain tolerance) and H was significant respiratory depression (a 50% increase in depression of ventilation). The proportion of subjects having significant antinociception at time t is denoted by πB(t); the proportion of subjects experiencing significant respiratory depression is denoted by πH(t). Hereinafter, we will use the term analgesia also for the antinociceptive responses observed in study 2.
The classic definition of utility function U, the probability of benefit minus the probability of harm, is given in this case by Boom et al. (2013):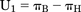 (1)The variance of U1 can be estimated by var{πB} + var{πH}, assuming the probabilities of benefit (analgesia) and harm (respiratory depression) are independent. The definition of utility first used by Roozekrans et al. (2018) is the probability of analgesia without harm (e.g., dizziness or respiratory depression). Its estimate is also a proportion:
(1)The variance of U1 can be estimated by var{πB} + var{πH}, assuming the probabilities of benefit (analgesia) and harm (respiratory depression) are independent. The definition of utility first used by Roozekrans et al. (2018) is the probability of analgesia without harm (e.g., dizziness or respiratory depression). Its estimate is also a proportion: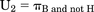 (2)Thus, the number of subjects having analgesia without harm is divided by the number of subjects.
(2)Thus, the number of subjects having analgesia without harm is divided by the number of subjects.
In Boom et al. (2013), it was recognized that the utility is dependent on the selected thresholds for benefit and harm. Therefore, in Roozekrans et al. (2018), we explored the impact of changing the threshold for analgesia, and by doing so were able to create so-called “utility surfaces,” where the thresholds for analgesia were depicted by different colors. First, the probability range of zero to one was divided into two ranges. The first range depicts the (estimated) probability of no harm with colors green to yellow and the second range depicts the probability of harm with colors orange to red. The changes in color were determined by the probability distribution functions, where these are functions of the threshold for analgesia. Thus, the empirical distribution is the proportion πB(t,θ), where θ denotes threshold. The thresholds are determined by the observed data. Depending on the levels of analgesia and harm, four extremes are defined: pain relief without harm [B+/H−, denoted by the color green in Roozekrans et al. (2018)], no pain relief and no harm (B−/H−, denoted by the color yellow), harm without pain relief (B−/H+, denoted by the color red), and finally harm with pain relief (B+/H+, denoted by the color orange). Gradients in between these extremes are depicted by corresponding colors depending on threshold θ. The R code for the construction of the utility functions is available from the authors (a.dahan{at}lumc.nl).
Results
Study 1.
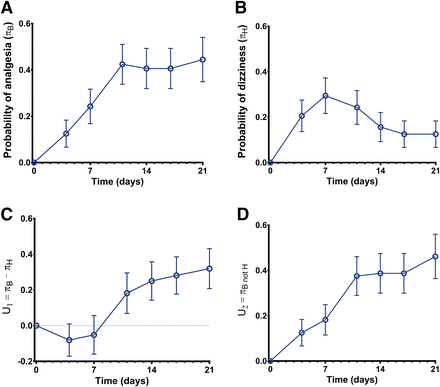
Twenty-four patients (70%) showed improvement of pain scores during the 3-week pregabalin treatment. Dizziness occurred in 13 patients (38%); of all reported side effects dizziness occurred most frequently. The probabilities of analgesia (πB) and dizziness (πH) are given in Fig. 1, A and B. The utility function U1 (eq. 1, i.e., benefit − harm) is given in Fig. 1C. The function is negative in the first week of treatment, indicative of the greater probability of adverse effect than analgesia, but positive thereafter. In Fig. 2, the utility surface is given. The probability of experiencing neither benefit nor harm from pregabalin treatment (yellow surface) decreases over time from 40% at day 4 of treatment to 15% on day 21; the probability of just harm peaks at day 7 (20%) and is <10% at day 21. The probability of just benefit (green and green/yellow surface) slowly increases over time from 40% at day 4 to 70% at day 21. However, when we apply the threshold of 50%, the probability of analgesia >50% was just 10% on day 4 and 45% on day 21 (deep green surface; see also Fig. 1D). The probability of benefit that coincides with harm was stable over time (approximately 10%; orange surface).
Utility functions of study 1. (A) Probability of pregabalin-induced analgesia (benefit, πB). (B) Probability of pregabalin-induced dizziness (harm, πH). (C) Utility function U1 = πB − πH or probability of benefit minus probability of harm. (D) Utility function U2 = πB and not H or the probability of benefit without any harm. Data are ± S.D.
Pragmatic utility surface of study 1. Depending on the levels of analgesia and dizziness, four extremes are defined: pain relief without dizziness (green), no pain relief and no dizziness (yellow), dizziness without pain relief (red), and dizziness with pain relief (orange). Gradients in between these extremes are depicted by corresponding colors.
Study 2.
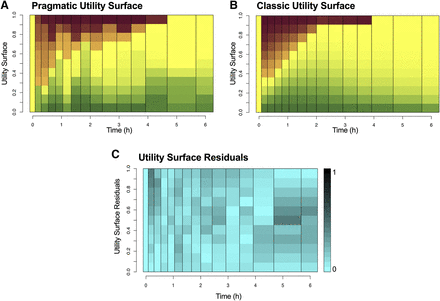
Antinociceptive responses and respiratory depression were observed in all participants, albeit with differences in magnitude and dynamics. The probability πB (increase in pain tolerance >50%) was between 20% and 30% during the first 4 hours after fentanyl administration (Fig. 3A). The probability function πH (reduction in minute ventilation >50%) declines from 0.75, just following fentanyl administration, to 0 at t = 5 hours (Fig. 3B), where U1 shows a nadir at t = 30 minutes (value of −0.5), after which the probability function slowly increases toward zero (Fig. 3C). The value of U2 (probability of just analgesia) ranges between 0 and 0.2 (Fig. 3D). The utility surface (Fig. 4) shows an initial high probability of harm without or with some analgesia (probability >70%; red and orange surfaces), which slowly declines toward 10% at t = 4 hours. The probability of just analgesia was low throughout the study period (<10%). The remaining surface (yellow) indicates neither analgesia nor respiratory depression and increases from 20% at t = 5 minutes to 100% at the end of the study, an indication that fentanyl concentrations at the effect site were low.
Utility functions of study 2. (A) Probability of fentanyl-induced antinociception (benefit, πB). (B) Probability of fentanyl-induced respiratory depression (harm, πH). (C) Utility function U1 = πB − πH or probability of benefit minus probability of harm. (D) Utility function U2 = πB and not H or the probability of benefit without any harm. Data are ± S.D.
Pragmatic (A) and classic (B) utility surfaces of study 2. Depending on the levels of analgesia and respiratory depression, four extremes are defined: pain relief without respiratory depression (green), no pain relief and no respiratory depression (yellow), respiratory depression without pain relief (red), and respiratory depression with pain relief (orange). Gradients in between these extremes are depicted by corresponding colors. (C) Residuals of the difference of the pragmatic and classic utility surfaces of study 2. The residuals range from 0 (light blue) to 1 (black).
Discussion
The desired effects of analgesics often coincide with a myriad of side effects that limit their usefulness in clinical practice due to reduced patient compliance and possibly actual bodily harm. Particularly, with increasing doses the probability of adverse effects increases. For example, at high doses, opioid analgesics produce respiratory depression that may at one point cause instability of the ventilatory control system with repeated apneic events and/or upper airway obstruction (Dahan et al., 2017b). To improve our understanding of the analgesic’s utility, it is important to capture the different behaviors of drugs into a single function. Such a function may be used to assess the utility of a drug in specific patient populations, determine the optimum dose regimen (e.g., the lowest-effective dose that coincides with still acceptable side effects), and allow comparison among drugs. Evidently, the time domain also needs to be considered since some effects and side effects vary over time as drug mechanisms are activated. The drug (or drug dose) with the highest utility U2 (i.e., a drug with little πH and high πB) is then the best choice. Although desired and undesired drug effects may be initiated at a single receptor system, signal transduction pathways may differ with consequently nonparallel concentration-response relationships. Hence, simply basing the drug’s utility on the therapeutic index (the ratio of concentrations causing toxic vs. therapeutic effects) is difficult since the ratio is dose dependent (Kharasch and Rosow, 2013).
The Concept of the Utility Function.
In recent years, multiple, often complex, models have been constructed to study the combined desired and undesired effect of drug treatment. For example, the well-being model combines positive and negative effects of anesthetic drug combinations (Zanderigo et al., 2006). We previously developed utility (or safety) functions based on the integrated positive and negative behavior of drug using a PK-PD modeling approach (Yassen et al., 2008; Boom et al., 2013; Dahan et al., 2017a; Roozekrans et al., 2018). As implied by Henthorn and Mikulich-Gilbertson (2018), these utility functions are not a formula or equation but rather an algorithm, which gives a string of values (i.e., a function in two or three dimensions) that accounts for both desired and undesired outcomes. In the case of our examples in studies 1 and 2, we created functions that give an objective calculation of the probabilities of analgesia with and without significant dizziness or respiratory depression (with value θ determining the threshold between nonsignificant and significant effects).
Our utility function is based on the economic principle that the benefit of an action comes at the cost of a specific harm, i.e., U = benefit − harm. This concept has previously been applied in medicine for determination of the utility of antihypertensive therapy by Sheiner and Melmon (1978) and anticoagulant therapy by Cullberg et al. (2005). To construct the utility function, we previously performed population PK-PD modeling studies (Yassen et al., 2008; Boom et al., 2013). These are complex studies that require the availability of PK data and modeling capabilities. Here, we propose a more pragmatic utility function based on the probabilities of benefit and harm.
Pregabalin and Fentanyl.
The results of our two examples are promising and the three-dimensional response surfaces (Figs. 2 and 4) give a clear indication of the utility of pregabalin and fentanyl in their respective study populations: middle-aged chronic pancreatitis patients and healthy young volunteers. Dizziness is an important side effect of pregabalin therapy and may result in falls and fractures, especially in elderly patients. We show that dizziness without analgesia has a probability of approximately 20% occurring throughout the 3-week treatment period with oral pregabalin. Significant analgesia without dizziness increased over time from 5% to 25%. On average, 50% of patients will experience either no or limited analgesic effects (yellow and yellow/green surfaces, Fig. 2), or have analgesia with dizziness (orange surface). We conclude from the utility surface analysis that utility of pregabalin treatment increases over time, and as such the patient should be kept on pregabalin treatment for an appropriate time period (2 to 3 weeks) to allow an accurate assessment of benefit versus harm (utility). Nonetheless, our results indicate that pregabalin is of limited efficacy in chronic pancreatitis patients when the aim of therapy is significant pain relief, i.e., more than 50% reduction of baseline pain. Accepting less pain reduction increases the utility of the drug to 50%–70% of patients; however, these effects coincided with dizziness in a large proportion of patients. On the other hand, reduction in pain intensity is only one aspect of the complex process of pain perception and different endpoints may show different results, as demonstrated in the original report where significantly more patients in the pregabalin-treated group rated their overall health situation as improved compared with the placebo-treated group (Olesen et al., 2011). This indicates that B may be redefined, for example, by using satisfaction with pain relief. Still, even then benefit and harm would coincide in the majority of patients.
Similarly, respiratory depression from opioids is important as well since it is potentially lethal, as is exemplified by the current opioid epidemic and large number of opioid deaths in the United States (Okie, 2010; Anonymous, 2018). In study 2, we tested the effect of intravenous fentanyl in opioid-naive healthy volunteers. As expected from the relatively high dose (3.5 μg/kg), the probability of fentanyl-induced respiratory depression without much or any analgesia occurs immediately following injection and dissipates slowly. Analgesia did occur but was invariably coupled to respiratory depression. This indicates that it is difficult to induce significant fentanyl analgesia without respiratory depression in this population. Further studies are needed to assess the utility function of potent opioids in chronic pain patients, since thus far studies have been limited to healthy volunteers and acute pain. Still, animal studies demonstrate that tolerance to opioid-induced respiratory depression may not occur when tolerance to analgesia has developed (Emery et al., 2016). We made similar observations in individuals that chronically use high-dose opioids (A. Dahan, unpublished data).
Utility of the Utility Function.
The use of the pragmatic utility function has one important drawback. Constructing utility functions that are not based on PK-PD models leads to inability to determine the utility as a function of concentration. Consequently, the effects of alternative dose administration regimens cannot be assessed. In study 1, for both functions U1 and U2, the highest utility was reached at 21 days of therapy (Fig. 1, B and C); U1 is initially negative (but not different from zero), while U2 is invariably positive. When U1 = 0, we can only state that the probabilities of significant analgesia and dizziness are equal, i.e., πB = πH. If these probabilities are independent, U2 has a maximum probability of 0.25 at πB = πH = 0.5 since U2 = πB and not H = πb ⋅ πnot H = πB ⋅ (1 − πH). This indicates that of the two functions (U1 and U2), U2 is the more informative about the actual drug utility. Finally, it is important to realize that utility functions U1 and U2 are context sensitive, i.e., they depend on the predefined threshold value, such as the threshold for significant analgesia). The utility surfaces (Figs. 2 and 4) give an even more complete picture since they incorporate multiple thresholds with information on all four possible outcomes that range from the most desired condition (B+/H− via B+/H+ and B−/H−) to the least desired condition (B−/H). On the other hand, utility surfaces are more complex, and if the functions are to be used in clinical practice U1 is the most intuitive (Dahan et al., 2015).
Comparison between Model-Based and Pragmatic Utility Surfaces.
Since the pragmatic and model-based (or classic) utility surfaces are based on different analytical approaches, we compared the two utility surfaces derived from study 2 (Fig. 4). First, we reconstructed the classic utility surface based on the measurement times (similar to the pragmatic utility function) (Fig. 4B), and then we calculated the difference in probabilities per time unit for the 11 squares per time unit (each representing a probability quantile). The residuals are given in Fig. 4C, with deeper levels of blue indicative of larger residuals. Since the residuals are relatively small (on average <0.1) and the larger residuals equally spread over the surface, we conclude that the two methods are comparable. Differences between the pragmatic and model-based utility functions are most likely caused by the fact that the model-based utility function by definition does not contain residual intra-individual error. Therefore, the pragmatic utility is more uncertain, and confounded by measurement error at baseline, which is the reference for determining benefit and harm; baselines are estimable parameters with the model-based approach. Still, the pragmatic utility function is sufficiently robust to be used as a potential standalone option for the analysis of drug effects.
We successfully constructed pragmatic utility functions based on the probability of two binary outcomes, significant analgesia and adverse effect. We foresee an important role for these functions in model-based development of analgesics with less severe adverse effects relative to their benefit than for current frequently used opioids (van der Schrier et al., 2017).
Authorship Contributions
Participated in research design: A. E. Olesen, Broens, S. S. Olesen, Niesters, van Velzen, Drewes, Dahan, Olofsen.
Conducted experiments: A. E. Olesen, S. S. Olesen, Broens, Niesters, van Velzen.
Contributed new reagents or analytic tools: Olofsen.
Performed data analysis: S. S. Olesen, Olofsen, Dahan.
Wrote or contributed to the writing of the manuscript: A. E. Olesen, Broens, S. S. Olesen, Niesters, van Velzen, Drewes, Dahan, Olofsen.
Footnotes
- Received September 19, 2018.
- Accepted November 12, 2018.
Abbreviations
- B
- benefit
- H
- harm
- PD
- pharmacodynamics
- PK
- pharmacokinetic
- π
- probability
- θ
- threshold
- U
- utility
- var
- variance
- Copyright © 2019 by The American Society for Pharmacology and Experimental Therapeutics